Les télescopes existants
Télescope de Newton
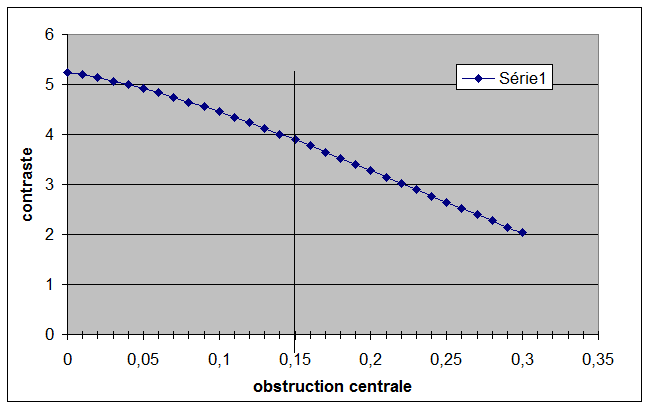
Le télescope de Newton moyennant quelques considérations sur l'ouverture et l'obstruction centrale constitue un télescope de choix. Aujourd'hui la portabilité et les montures allemande du commerce font que l'on privilégie les rapports d'ouverture F/D faible 4 ou 3.5. Avec de telles ouvertures la qualité optique du primaire peut laisser à désirer et l'on a forcement une obstruction centrale relativement importante. L'ALPO considère le contraste C dans la tache d'Airy en faisant le ratio entre l'énergie dans le pic centrale et l'énergie dans l'ensemble des anneaux.

Pour une obstruction nulle 84% de l'énergie est dans la tache centrale et on a C=0.84/0.16=5.25
On voit que le contraste dans l'image est divisé par 2 pour une obstruction de 0,25. Par ailleurs l'obstruction rends le télescope plus sensible à la turbulence. Il est admis (Texereau) qu'une obstruction de 0.16 fournis des images indiscernables d'une image obtenue sans obstruction à condition que le télescope soit fermé.
"pour les télescopes l'obstruction centrale rend l’instrument également un peu plus sensible à la turbulence, seul un télescope fermé de bonne qualité et à obstruction inférieure à 1/6 D est assimilable à un bon réfracteur à f / 12 pour cet usage"
La fermeture du télescope par une lame optique avec un tube ne rayonnant pas vers l'intérieur permet de s'affranchir des problèmes de turbulence de tube spécifique des Newtons. Voici ce qu'en dit Texereau (CTA2 P161):
"il apparaît que le principal inconvénient du télescope, comparé à une lunette, est une sensibilité plus grande aux effets thermiques instrumentaux due à l'ouverture supérieure du tube. Il faut distinguer deux effets nuisibles :
1° L’air extérieur brassé par le vent, qui pénètre librement dans le télescope, provoque des échanges thermiques rapides avec les parois du tube, surtout si elles sont métalliques, d'où création de veines d’air à températures donc indices de réfraction un peu différents et déphasage locaux variables et mobiles, Des volutes lents s'élèvent toujours des pièces massives du télescope, sans oublier le miroir principal. De véritables tourbillons turbulents résultent de l'attaque du vent à la bouche de l'instrument.
2° Supposons le milieu ambiant assez stable pour permettre une bonne égalisation thermique malgré la grande inertie du télescope. Les brutaux échanges par convection disparaissent mais il subsiste inévitablement le rayonnement des surfaces. En particulier le miroir lui-même rayonne vers le ciel, comme le tube, le miroir secondaire et ses lames support ; toutes ces pièces sont entourées de gaines d'air où le gradient d'indice peut correspondre, très localement heureusement, à des déphasages de
l / 2 ! Ces gaines d'air sont parfaitement stables, aucune turbulence n'est observable de ce fait mais le premier anneau de la tache de diffraction est très notablement renforcé, inconvénient d'autant plus sensible qu'il s'ajoute à celui de l'obstruction centrale. De plus le miroir qui rayonne vers le ciel présente en général une aberration de sphéricité appréciable particulièrement dans le cas d’un disque important assez épais ayant souvent des résidus de trempe."Le spot diagram et la MTF d'un newton de 300mm fermé avec une lame à faces parallèles, ouvert à F/6 et une obstruction de 0,16 est donnée ci dessous:
on voit que le champ est dominé par la coma. Le champ limité par la diffraction est faible typiquement 4 ou 5 minutes d'arc d'où la nécessité d'avoir une collimation stable.
Dall Kirkam
Les télescopes type Cassegrain sont à priori bien adaptés à l'imagerie haute résolution. La variante avec miroir secondaire sphérique mis en vogue par Takahashi avec la série Mewlon présente
une coma très forte (10 fois celle du Cassegrain classique) par contre la combinaison est moins sensible au désalignement du secondaire et le primaire est moins déformé (-0.7) que le primaire d'un Cassegrain d'ou une optique plus facile à réaliser avec une bonne précision. Le spot diagram et la MTF sont calculés pour une combinaison à F/16
on voit sur la MTF l'impacte de l'obstruction centrale et la dégradation rapide du champ.
Ritchey Chrétien RC
Les newton ou Cassegrain sont fortement affectés par la coma on peut donc considérer que la combinaison RC ou la coma est corrigée est une solution attractive. Avec la combinaison classique à F/8 (primaire à F3) on a le spot diagram ci dessous. L'obstruction centrale est importante ainsi que la déformation du secondaire qui le rends difficile à réaliser. Sinon le champ corrigé est bien plus important.
On peut optimiser le RC pour l'observation planétaire en diminuant l'obstruction centrale et en augmentant le rapport F/D. Voici un exemple avec un secondaire de 64mm et un F/D de 13
la déformation du primaire est de -1.026 et celle du secondaire -2.7 le primaire à F/3 reste néanmoins très difficile à faire par un amateur.
On peut partir d'un primaire à F/4 mais dans ce cas on a des focales de l'ordre de 7m et des problèmes d'échantillonnage avec les cameras CMOS actuelles qui ont de tout petit pixels.
Lunettes
avec une lunette on ne peut guère aller au delà de 200mm de diamètre. Les combinaisons apochromatiques sont hors de prix donc il reste un doublet classique style Fraunhofer avec des verres type BK7-F2. un exemple à F/20 replié par des miroirs plans est donné ci dessous:
La MTF poly chromatique est très loin de la MTF idéale.
Avec un doublet apo (ZK7- FPL55) de 200mm à F/15 replié voila ce que l'on aurait:
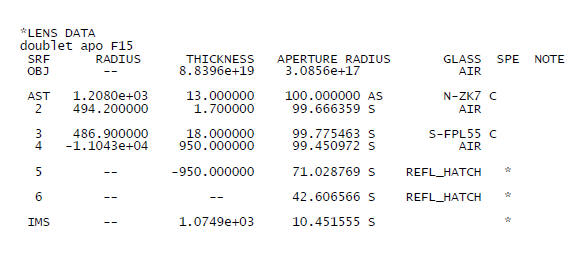
On voit dans ce cas que la MTF est pratiquement parfaite, j'ai limité le champ à 24' il est pratiquement équivalent sur 30 minutes. On peut donc prendre une image de la lune en entier tout en étant optiquement parfait.
Wright camera
Ce télescope n'est pas considéré pour la haute résolution. Il en a pourtant les attributs intéressants, il est fermé, il n'a pas de coma et est insensible de ce fait à la de-collimation. On peut le concevoir avec un secondaire de petite taille pour maximiser le contraste. Le télescope de 300mm à F/6 a les performances suivantes:
l'obstruction est de 0,16 et le champ de pleine lumière est de 18'. Pour diminuer la taille du tube la lame correctrice est rapprochée du primaire dont le coefficient de déformation est de +1,1
le primaire n'est pas parabolique mais ellipsoïdale. Le coefficient de déformation positif fait que le miroir comme la lame de fermeture peuvent être taillés par la technique de dépression. On voit que la MTF est aussi bonne qu'avec une apo (mais ici en 300mm avec une focale de 1800mm). On observe encore très légèrement l'effet de l'obstruction centrale. Moyennant un peu de vignetage on peut prendre la lune en entier en conservant cette qualité.
On peut raccourcir le télescope à F/5 au lieu de F/6 mais l'obstruction est un peux plus forte et les optiques sont plus délicates à réaliser.
En changeant le miroir plan on a également un télescope grand champ intéressant qui couvre un champ de 44mm de diamètre (format 24*36) avec une image limité par la diffraction. Le miroir plan fait alors 76mm de petit axe. Le diamètre du champ couvert est de 1.4° . Le spot diagram est présenté ci dessous:
Avec deux miroirs plans on a donc un télescope très versatile.
Voyons la réalisation d'un tel télescope.
Cahier des charges
La qualité optique du télescope est une nécessité absolue pour atteindre des performances optimum. Par ailleurs la sensibilité à la turbulence est d'autant plus forte que la tolérance de l'optique est faible. Une qualité optique de l'ordre de lambda/8 (strehl 0.985) de la combinaison est souhaitable. Voyons ce que cela veut dire:
_Au niveau du plan on peut prendre ce qui se fait de mieux compte tenu de sa petite taille, typiquement Lambda/30 PV chez antares (lamba/15 sur l'onde)
_Au niveau de la lame compte tenu du facteur 0.5 sur la précision d'une lame par rapport à un miroir ( pour un miroir un écart de δe sur la surface conduit à un écart de 2δe sur l'onde, pour la lame une erreur de δe produit une erreur de (n-1)δe sur l'onde, compte tenu des deux faces l'erreur est de 2(n-1)δe soit une sensibilité de (n-1) de la lame par rapport au miroir) on se donne donc une précision double pour la lame que pour le miroir.
_ Suivant la précision du miroir primaire voyons ce que cela donne au niveau de la combinaison totale
Si on calcul l'écart type de l'onde issue de la combinaison on a σ = racine(σ2lame+σ2primaire+σ2secondaire)
On prend à titre indicatif (compte tenu de la façon dont les surfaces vont être faites) σ = PV/3.5
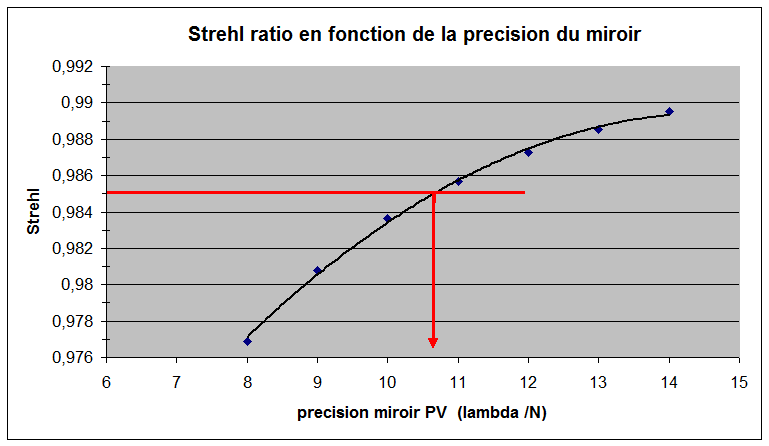
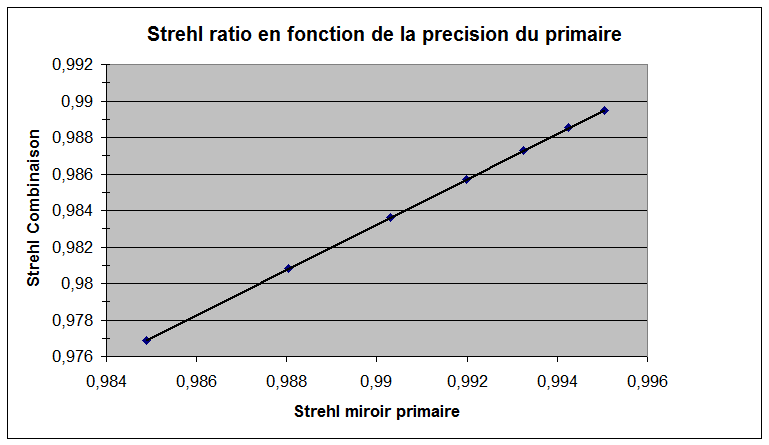
On voit qu'il faut un miroir ayant une précision minimum de λ/10 (strehl 0.99) et une lame avec la même précision sur les surfaces soit λ/20 en transmission
pour obtenir une combinaison complète à λ/8
j'ai choisi de réaliser le primaire à F/D=6 plus tolérant que la solution à F/D=5
Réalisation des optiques par dépression
La combinaison optique comporte un miroir elliptique de coefficient de déformation +1 et une lame correctrice. Pour rapprocher la lame du primaire, raccourcir le tube et faire porter le secondaire sur la lame j'ai ajusté le coefficient de déformation bs à +1.1
le coefficient de déformation du miroir étant positif on peut obtenir la forme par la méthode de dépression. Ce qui doit assurer une surface très douce.
On a l'équation de la surface du miroir: 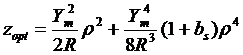
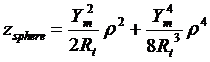
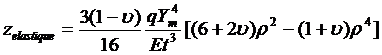
![]()
avec
Rt rayon de courbure de l'outil
R rayon de courbure du miroir primaire
Ym rayon utile du miroir
bs coefficient de déformation du miroir
q dépression
E module de Young du substrat
t épaisseur du miroir (ménisque)
υ coefficient de Poisson du substrat
en égalant les termes en ρ4
on obtient la dépression à appliquer: 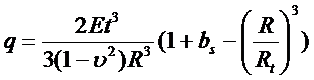
en égalant les termes en ρ2
on obtient le rayon de courbure de l'outil: 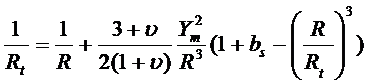
on pose:
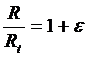 d'où
d'où
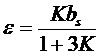 avec
avec
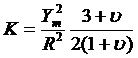

Le calcul précèdent est valable pour un ménisque d'épaisseur constante.
En appliquant la théorie de Lemaitre [31] développée pour la déformation des lentilles on peut comparer l'aberration sphérique d'un ménisque sous contrainte ou d'un miroir à dos plat sous contrainte. Ces deux cas sont représentés ci dessous.
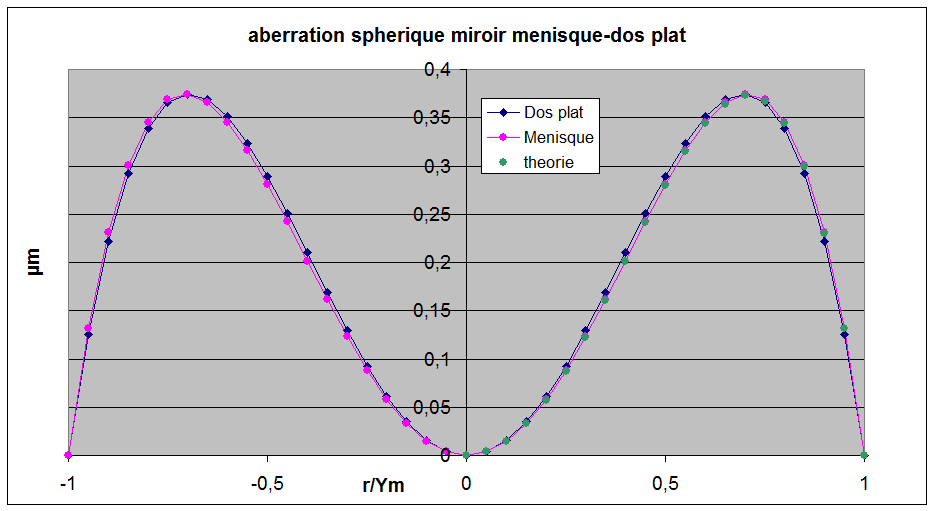
On voit sur la figure ci dessus que la déformation du ménisque (courbe rose) est en parfait accord avec la déformation théorique du miroir (courbe verte ) par contre dans le cas d'un dos de miroir plat il y a un écart sensible représenté ci dessous:
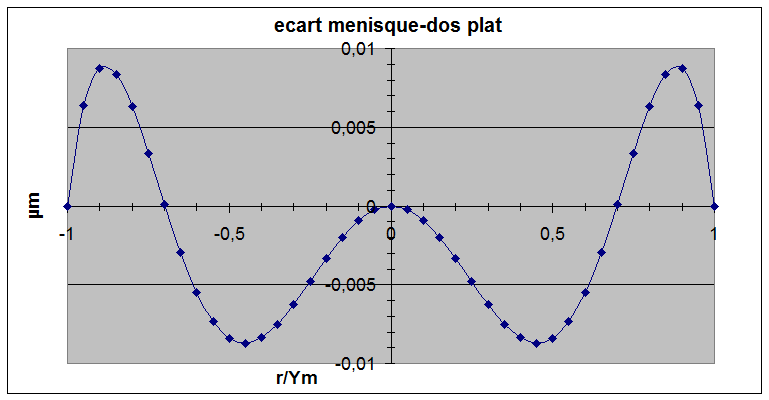
L'écart sur la surface atteint 0.018µm PV soit 0.036µm sur l'onde ou λ/15. Bien que l'erreur soit inférieur à la précision cherchée, pour éviter de cumuler les erreurs d'exécutions avec les erreurs de méthode, j'ai pris l'option de tailler un ménisque bien que le temps d'ébauchage soit double par rapport à celui d'un miroir avec un dos plat.
Les conditions de pression pour asphériser le miroir sont indiquées dans le tableau ci dessous:
| Miroir elliptique | ||||||
| E | 7,75E+10 | pa | ||||
| nu | 0,17 | |||||
| Focale miroir | F | 1800 | mm | flèche | 3,12635752 | mm |
| D | 300 | mm | ||||
| r^4/t2 | 6944,4 | |||||
| Ym | 150 | mm | ||||
| Ym/2R | 0,020833333 | mm | ||||
| coefficient de déformation | bs | 1,10 | ||||
| R | 3600 | mm | ||||
| épaisseur Ménisque | t | 27 | mm | |||
| K | 0,002351911 | |||||
| eps | 0,002568976 | |||||
| rayon outil | Rt | 3590,775383 | 3,13439606 | |||
| écart à la sphère | 0,000372993 | 373,0 | nm | |||
| dépression (atm) | q | 0,249 | atm | |||
| 2,49E+04 | pa | |||||
| déflexion | 6,64 | µm | ||||
Le matériaux choisi pour la réalisation du miroir et pour son faible coefficient de dilatation est du quartz . Les opérations à mener sont les suivantes:
_On commence par tailler le miroir sphérique.
_ Ensuite, on le met sous pression (0.249atm) (déflexion de 6.6µm mesurée au sphéromètre) puis on le taille de nouveau sphérique avec le polissoir pressé sur le miroir contraint. Il faut enlever les 373nm d'asphéricité induite par la mise sous pression pour q'une fois dé contraint le miroir ait la bonne forme.
Le seul point à soigner particulièrement, car il n'est pas automatiquement obtenu avec la méthode est l'astigmatisme. Pour l'éviter au mieux on tournera le miroir systématiquement sur son support entre deux séances de polissage.
Taille de la lame:
Les conditions de pression pour tailler la lame sont les suivantes:
| Feuille de calcul pour l'exécution d'une lame correctrice | ||||||
| Jean Dijon | ||||||
| Données Mecaniques | ||||||
| 1 | module young | 7,27E+10 |
Pa |
borro 33 | ||
| 2 | Coefficient poisson | 0,23 | ||||
| 3 | equation de la lame à realiser: | y=M A(ρ4-kρ2) | ||||
| Données à modifier | les cases en gris sont à renseigner | |||||
| 4 | rayon utile de la lame | Ym | 145 | mm | ||
| 5 | indice du verre | n | 1,4714 | |||
| 6 | Focale du télescope | F | 1800 | mm | ||
| 7 | Coefficient k' de la lame | k' | 0,966 | à modifier jusqu'à ce que k ait la valeur cherchée | ||
| A | 0,005024756 | |||||
| 8 | Déformation par rapport à la lame de Schmidt | M | 2,10083234 | |||
| 9 | épaisseur de la lame | e | 15 | mm | ||
| 10 | rayon de l'appuis du support | a | 147,5 | mm | ||
| 11 | nombre de faces déformées | 2 | ||||
| 12 | Rayon du sphéromètre | rsphero | 145 | mm | ||
| 13 | poids de l'outil (optionnel) | 0,25 | kg | |||
| Résultats | ||||||
| 14 | Dépression dans le réservoir | p | 0,165 | atm | ||
| 15 | surpression due à l'outil | po | 0,000 | atm | ||
| 1/Rs | 2,22676E-06 | |||||
| 16 | Rayon de l'outil de taille | Rs | 449083 | mm | convexe | |
| 17 | Flèche de l'outil (pour r=rsphero) | r2/2/Rs | 0,0234 | mm | ||
| 18 | déflexion théorique de la lame pour r=a | wo | 0,0240 | mm | ||
| 19 | déflexion de la lame pour r=rsphero | wmesure | 0,0234 | mm | ||
| 20 | déflexion optimum de la lame (pour r=rsphero) | wo corrigé | 0,0234 | mm | ||
| 21 | coefficient k compte tenu du rayon utile | k | 1,000 | 1,000968122 | ||
| 22 | flèche de la lame hors contrainte | f | 0,00 | µm | convexe | |
| 23 | épaisseur maximum avant rupture | emax | 67,88 | mm | ||
On peut partir d'une lame à faces parallèles (doucie). On déprime alors la lame de 23µm en son centre et on la taille avec un outil ayant la même courbure (449 m) puis on la polie sphérique.
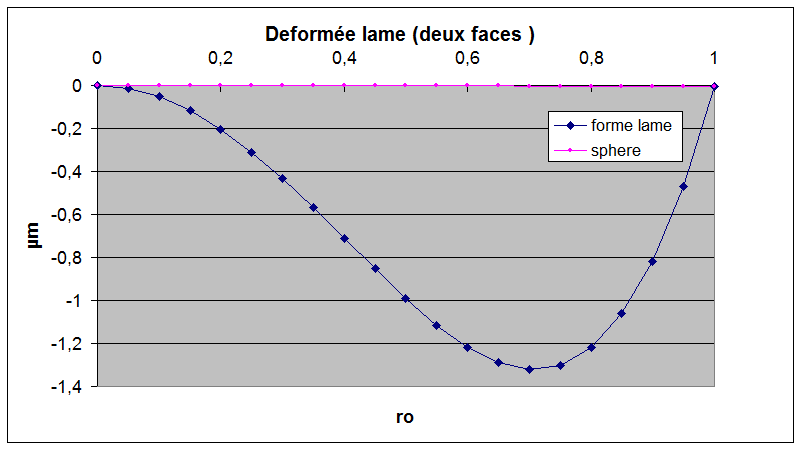
Compte tenu de la déformation (1.3µm par face) on pourrait sans doute la réaliser directement au polissage sans passer par une déformation avec des abrasifs.
On fait cette opération sur les deux faces en tournant la lame de 90° entre les deux opérations. Ceci minimise les problèmes d'astigmatisme de la lame du à la "casserole".
La "casserole" est celle utilisée pour tailler la lame du télescope de Backer .

Contrôles:
La stratégie pour contrôler les pièces est la suivante:
_ Tailler le miroir sphérique puis déformation du miroir sous pression pour obtenir une déformation bs=+1.1
_ Contrôle soigné de l'astigmatisme résiduel du miroir (interféromètre)
_ Tailler la lame par dépression et la contrôler contre le miroir, en double passage la déformation est de (-4.20+1.1) h2/Rmiroir le test est très sensible. Dans le télescope on auras bien une déformation de 1.1-2.1= -1 de la combinaison
Si le miroir n'a pas exactement un coefficient de 1.1 on ajuste la lame en conséquence (adaptation des deux surfaces)
Barillet:
Le miroir étant relativement mince (27mm) un barillet avec des leviers astatiques est nécessaire. Un barillet à 6 points sur la périphérie plus un point central est suffisant jusqu'à R4/e2 = 12000 [24], dans notre cas R4/e2 = 7000 donc un tel barillet convient.
En utilisant les équations de Couder on peut calculer le profil du miroir dans son barillet, la feuille Excel pour faire cette simulation est ici . Avec cette feuille on peut faire le calcul pour n'importe quel miroir avec un barillet comprenant jusqu'à 3 cercles concentriques de leviers astatiques. Pour éviter au mieux l'astigmatisme on place les points de contacts à la périphérie du miroir [24]
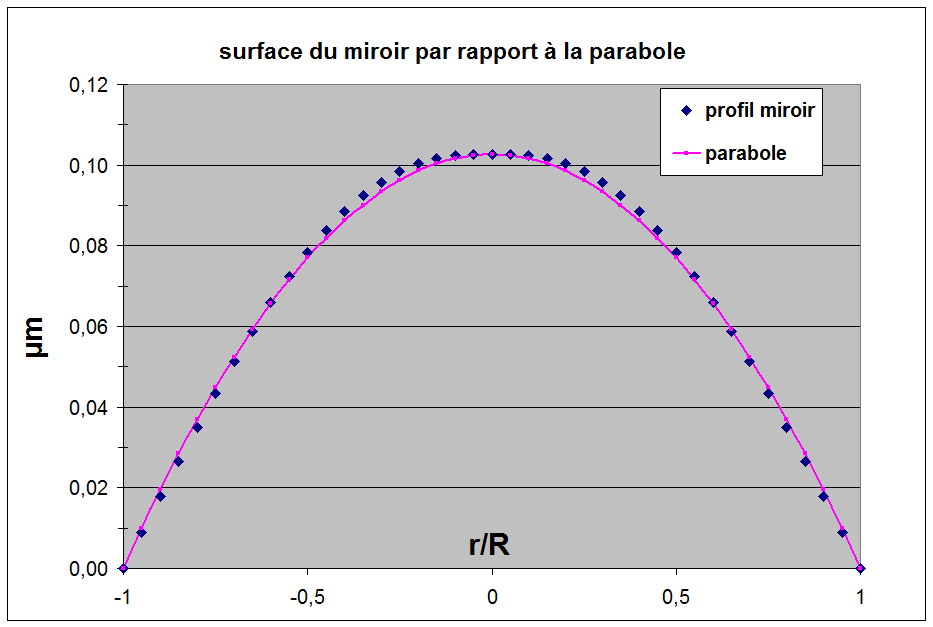
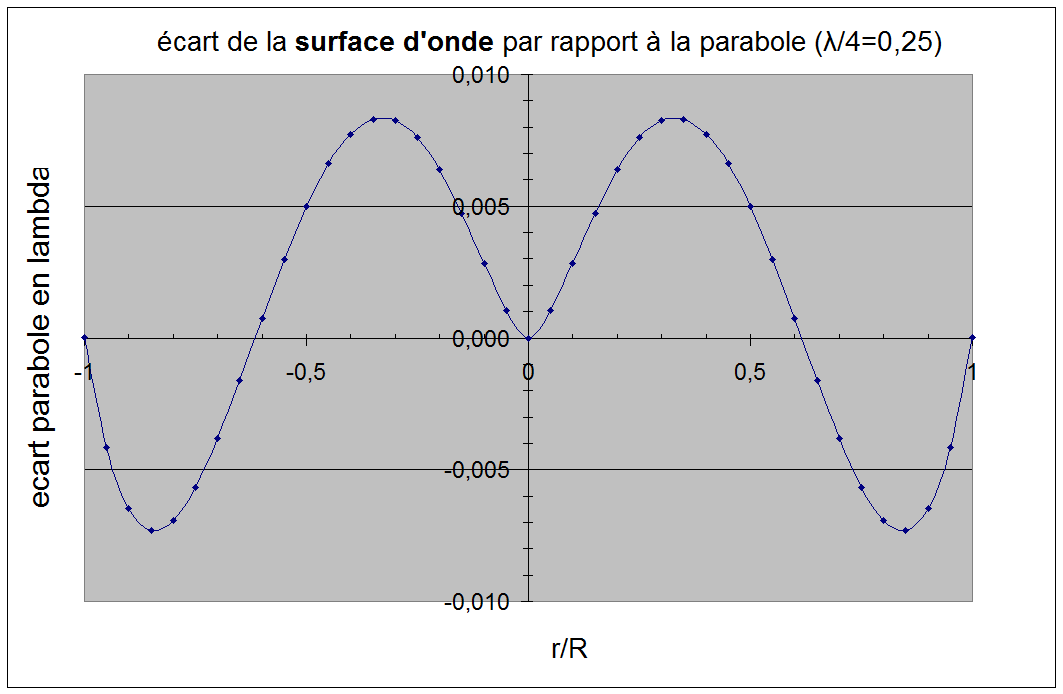
L'écart PtV de la surface d'onde par rapport à la parabole est de 0.016 λ au zénith (λ/60 ou 9nm). Le poids sur le levier central est de 615g et de 538g sur les 3 leviers de la périphérie. La courbure du miroir change de 0.1µm soit une variation de la mise au point de 50µm entre le zénith et l'horizon.
Un barillet avec deux cercles de leviers permettrait d'annuler le changement de courbure, mais une telle complication ne parait pas nécessaire.
Réalisation des pièces optiques:
J'ai réalisé deux outils en plâtre staturoc et carreaux de grés ceram de 25*25mm pour tailler les deux faces du miroir.
Outil convexe à gauche et outil concave à droite
Le quartz étant beaucoup plus dur que le verre l'ébauchage au carbo 80 a demandé environ 10h par faces.
Le doucissage est également beaucoup plus long. j'ai du gratter le plâtre avec une fraise de dentiste autour des carreaux pour éviter les rayures induites pas des grains d'émeri précèdent.
Miroir en cours de doucissage, la face arrière convexe repose sur l'outil concave avec un molleton épais entre les deux surfaces.
Le doucissage a été conduit jusqu'a une taille de grain de 5µm. Il est terminé le 22/09
Le doucissage terminé, la portée de la casserole a été rodée avec de l'émeri de 5µm pour que le dos du miroir (sphérique) s'adapte parfaitement et que l'étanchéité au vide puisse être faite.
Un essais après graissage de la porté montre que le vide statique est bon. Il n'y a pas de remonté de la pression pendant 12 heures. Le système est donc fonctionnel .
Photos ci dessus: miroir doucis sur la casserole permettant de le déformer par dépression. La flèche induite par la dépression max du système est de l'ordre de 15µm alors que le calcul montre qu'une flèche de 7µm est nécessaire. Tout semble donc correcte et la déformation sera réalisable. La difficulté sera d'obtenir une dépression répétable pour faire tourner le miroir par rapport au support. On verra le moment venu!
Il faut maintenant faire le polissoir pour polir le miroir sphérique.
Le polissoir a été réalisé avec des carrés de poix de 30mm
Le polissage du quartz avance bien moins vite que celui du verre.
Le polissage au cérium puis au blanc a pris environ 15heures. Le miroir était légèrement parabolisé à cette étape (b=- 0.4). j'ai décidé de démarrer le polissage sur la casserole le miroir ayant une forme régulière.
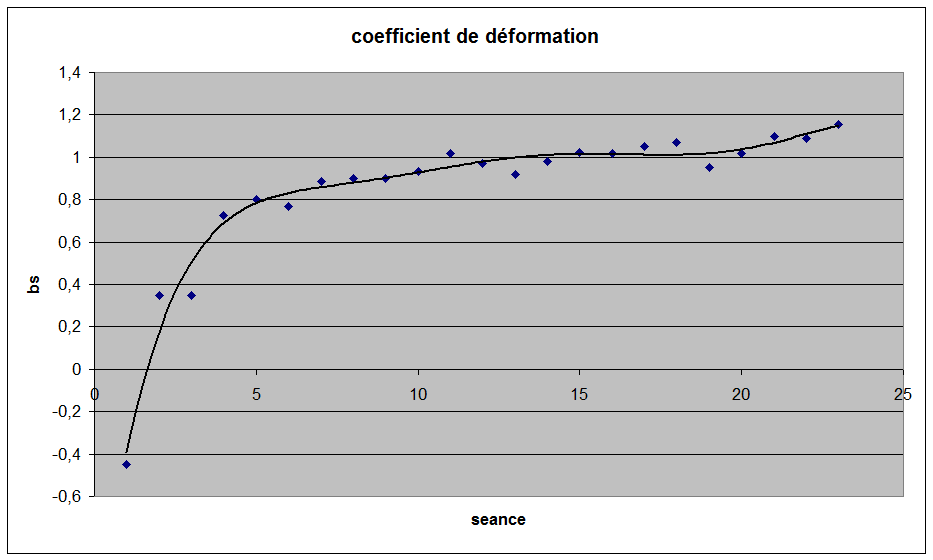
J'ai fait un nombre important de séances (j'ai fait des essais de polissage...) et l'on voit l'évolution du coefficient de déformation. Je suis resté longtemps autour de 1 puis j'ai décidé d'aller vers 1.15 qui est le coefficient idéal compte tenu de la position de la lame pour supprimer complètement la coma.
J'ai poli avec un mélange de blanc plus opaline à 50% . Ceci explique le nombre important de séances pour obtenir la déformation.
Le Foucault gramme du miroir st donné ci dessous (à gauche).
plusieurs problèmes subsistent: bord rabattu qui nécessite de diaphragmer le miroir à 295mm zones concentriques faibles mais présentes. On voit la déformation du miroir inverse de celle d'un miroir parabolique (image de droite)
miroir de Wright run1 miroir parabolique
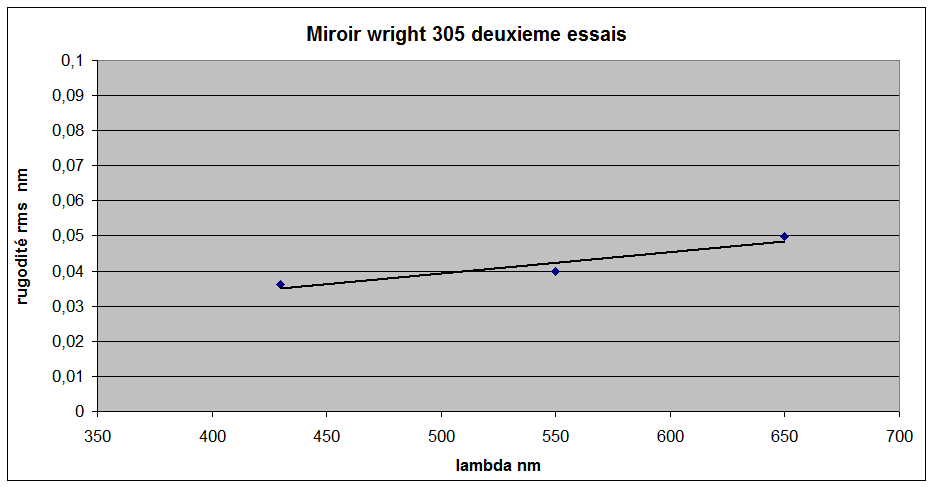
La rugosité est excellente: test de Lyot
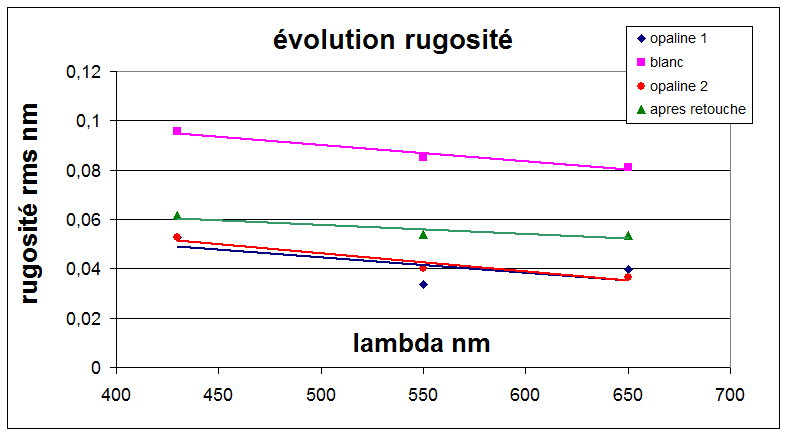
A gauche image du miroir en contraste de phase , à droite évolution de la rugosité mesurée en fonction du produit à polir
Avant l'opaline cf figure de droite, la rugosité est voisine de 1A rms on voit que les mesures en rouge vert bleu sont cohérentes
Après l'opaline on gagne un facteur 2 sur la rugosité et après quelques retouches finales on a une rugosité intermédiaire.
Par rapport à mes résultats sur verre obtenus dans les mêmes conditions de test on gagne sur le quartz avec la même technique de polissage un facteur supérieur à 2. Probablement due à la vitesse de polissage plus faible compte tenue de la plus grande dureté du quartz et à la forme sphérique.
Pour contrôler l'astigmatisme j'ai réalisé un interféromètre de Williams dont le principe est ci dessous:
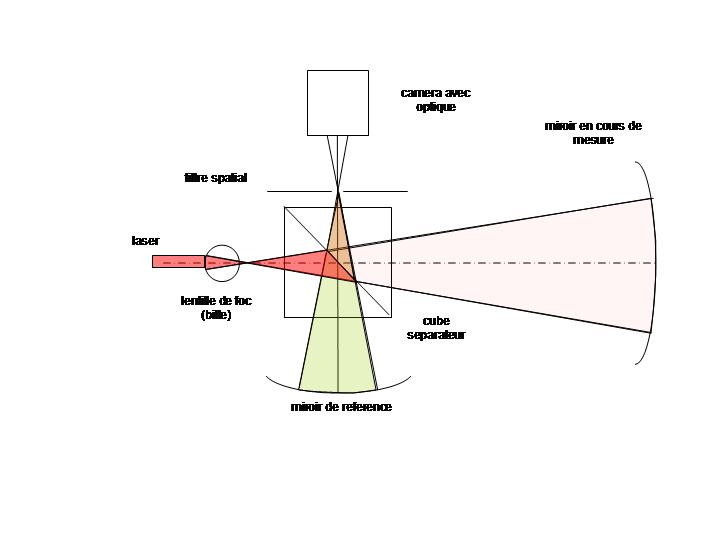
Les tests on été décevant avec un astigmatisme mesuré important de l'ordre de lambda/2
Après pas mal d'essais incohérents pour supprimer l'astigmatisme. j'ai décidé de retailler le miroir en prenant un soin extrême au niveau de la qualité de l'appuis de la casserole et du dos du miroir j'ai fini le doucissage du dos jusqu'a l'émeri 6µm et j'ai rodé le bord de la casserole avec cet émeri puis juste à l'huile en utilisant la rugosité du verre. Je ne peut pas faire mieux
j'ai repoli le miroir pour supprimer la déformation et j'ai recommencé le processus en tournant systématiquement le miroir par rapport à la casserole tout les 1/4 d'heure
Comme la pression est forte pour obtenir la déformation je règle la pression avec le manomètre après rotation du miroir. La forme obtenue au Foucault est bonne sans mamelonnage excessif le le bord rabattu est inexistant. La rugosité de 0.5Angstroem rms est équivalente à celle obtenue lors de la première déformation.
Au niveau astigmatisme ce n'est pas mieux qu'avant ce qui est très étonnant. J'en suis venu à douter fortement des mesures à l'interféromètre. Pour en avoir le coeur net, j'ai réalisé avec une étoile artificielle de 9µm un montage pour observer la tache de diffraction. J'utilise une lame semi 50% , 50% pour que la source soit sur l'axe optique car les essais avec la source hors axe montrent un astigmatisme. Voila le dispositif:
Avec ce montage, un léger astigmatisme de pliure du miroir est observé, astigmatisme qui ne tourne pas lorsque le miroir tourne j'en conclue que j'ai essentiellement un problème de support du miroir en position verticale. Ce problème combiné avec un astigmatisme variable du sans doute aux réglages de l'interféromètre explique certainement le manque de cohérence des mesures d'astigmatisme que j'ai obtenu avec l'interféromètre. J'attends d'avoir la lame pour vérifier sur le ciel si le miroir est bien OK.
En supprimant l'astigmatisme le test à l'interféromètre fournit un miroir ayant un coefficient de déformation de 1.06 (moyenne que j'ai obtenu avec plusieurs mesures) et un rapport de strehl autour de 0.97
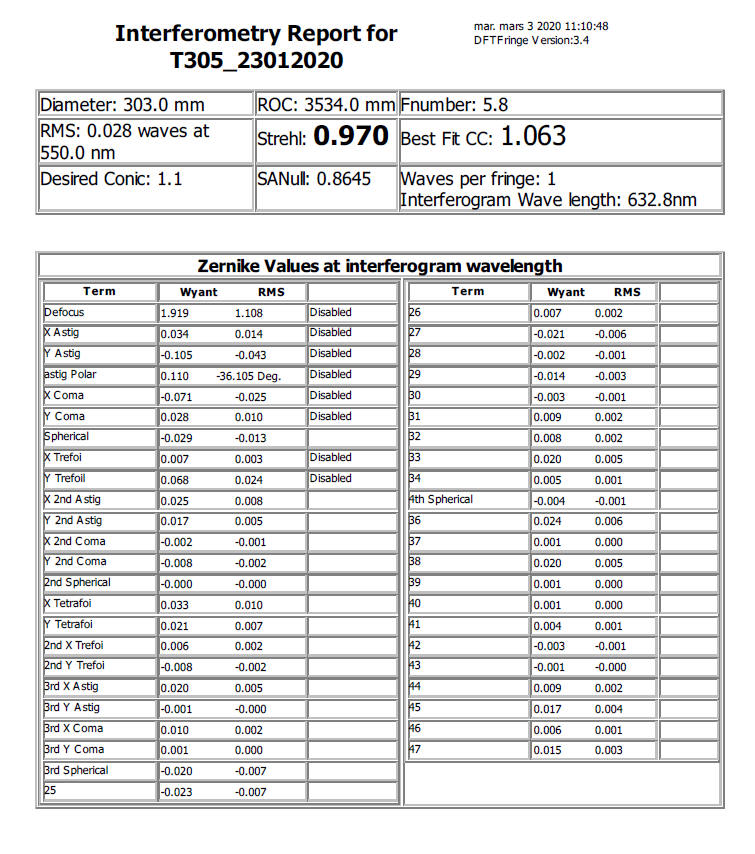
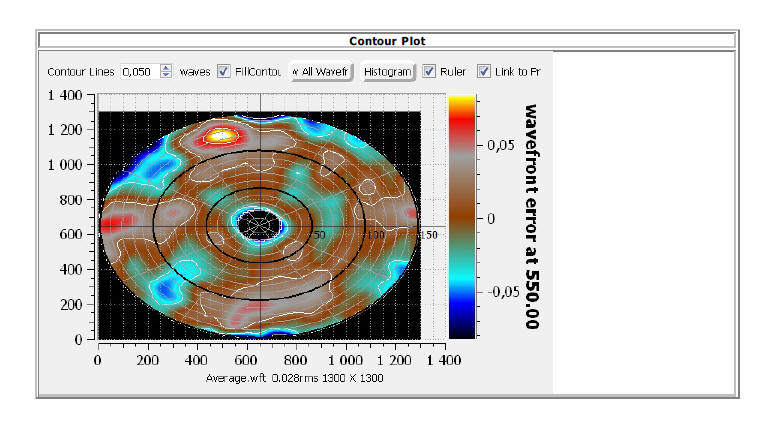
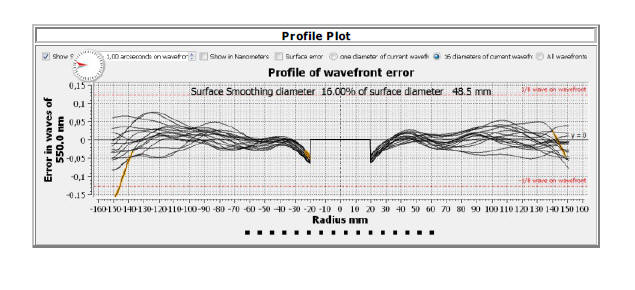
Je taille la lame pour compenser la déformation du primaire soit avec un coefficient de déformation de -2.06. Le miroir est un peu en deçà de ma spécification de départ mais j'en suis très proche.
Taille de la lame par dépression:
Après avoir réglé le parallélisme et la planéité des faces au
carbo 400 ( variation d'épaisseur sur la périphérie de l'ordre de 3µm et
planéité des faces au µm )
j'ai décidé de déformer la lame sur les deux faces, le polissage plan d'une
lame de 310mm et de 15mm d'épaisseur ne me paraissait pas si simple.
Le calcul pour atteindre la bonne déformation me donne une flèche de la lame
de 25µm à obtenir par dépression. J'ai donc taillé l'outil en verre convexe
qui servira à doucir la lame sous dépression. Cet outil a une flèche de 25µm.
J'ai réalisé la déformation des deux faces avec de l'émeri 10mn puis j'ai
continué
le doucissage au 20mn, 40mn. J'ai terminé avec du corindon de 3µm. La
valeur de la dépression est de 0.165 atm que je règle en mesurant la flèche de
la lame (25µm sur 295mm). Il n'y a aucun pb de régularité de la pression c'est
un vide statique et la chambre a un volume faible. Au niveau étanchéité la
portée doit être très bien rodée car c'est elle qui assure la condition
d'appuis qui défini la déformation élastique de la lame.
Ma portée fait 5mm de large, je l'ai rodé très finement avec de l’émeri 3µm et
j'ai fini en la rodant à l'huile avec le dos doucis de l'outil qui ma servi à
tailler la lame plane et parallèle. Ensuite je met une très fine couche de
graisse (roulement à billes) pour faire l'étanchéité. Je n'ai aucune évolution
de la flèche de la lame en 24h après mise sous vide.
Tout s'est bien passé au doucissage et la lame doit maintenant avoir sa forme
ébauchée (la déformation totale par rapport au plan est de l'ordre de 2.5µm)
j'ai réalisé le polissoir pour polir les deux faces de la lame simultanément
sur l'outil ayant servit à doucir la lame. La lame en borro33 devrait se polir
plus vite que le quartz.
Le polissoir de la lame
Après 8h de polissage sur une face et 4h sur l'autre, le poli avance bien sauf au centre ou le gris est plus long à partir comme le polissage se fait uniquement lame dessous. Je suis encore très loin d'un poli complet. Voila la lame sur la casserole en cours de polissage (au cérium)

Il m'a fallu 15 h de polissage par face pour supprimer le gris au centre car comme le polissage se fait exclusivement lame dessous le centre avance moins vite que le bord, j'ai poli avec du blanc à partir de 12h de polissage.
Au premier contrôle j’étais sur corrigé, ce que j'ai amélioré assez rapidement en diminuant la pression. Mon objectif est d'avoir la combinaison complète (miroir+ lame) à au moins Lamba/10 Ptv.
j'ai fait toutes les corrections sur une seule face, avec un outil couronne pour diminuer une zone de 150mm de diamètre et j'ai travaillé le bord avec l'outil pleine taille pour supprimer en particulier le léger bord rabattu du miroir. J'ai fait les mesures avec Virtual couder qui est très précis.
Sur le miroir, que j'avais mesuré à l’interféromètre (coefficient de déformation +1.06 strehl 0.97 ) je retrouve bien le coefficient de +1.06 et je trouve une erreur Ptv de L/17 avec un léger anneau de 120mm de diamètre ce que me donne l’interféromètre.
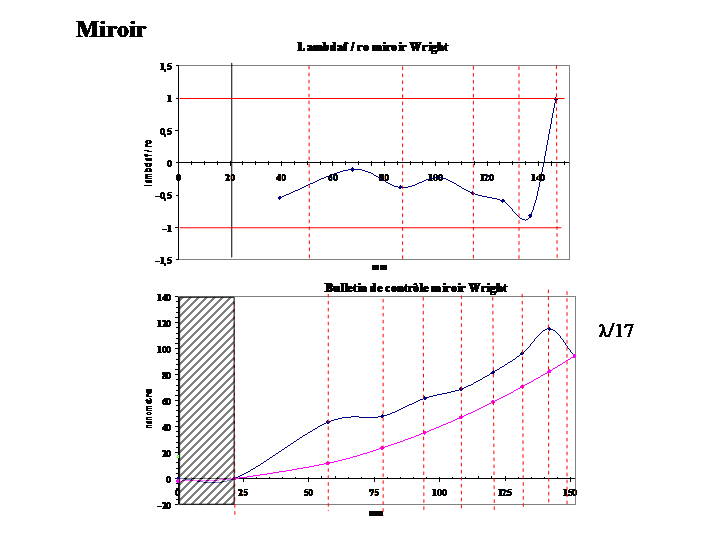
Le Foucault de la lame sur le miroir (double passage dans la lame) montre une surface très douce:

Foucault de la lame sur le miroir
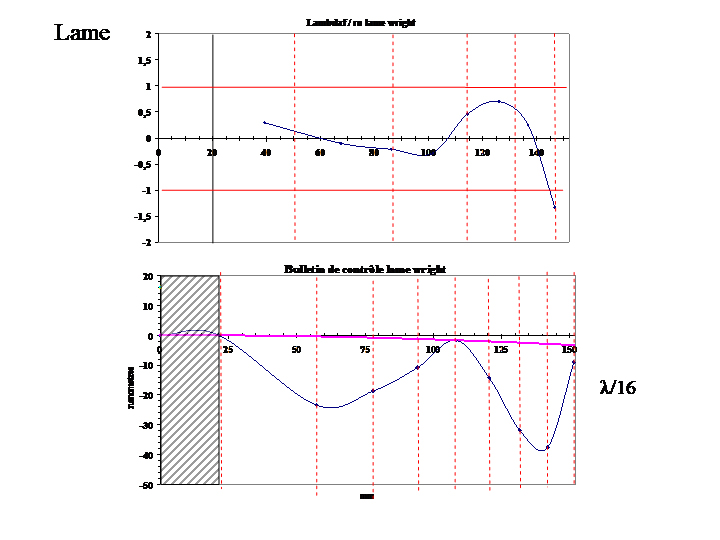
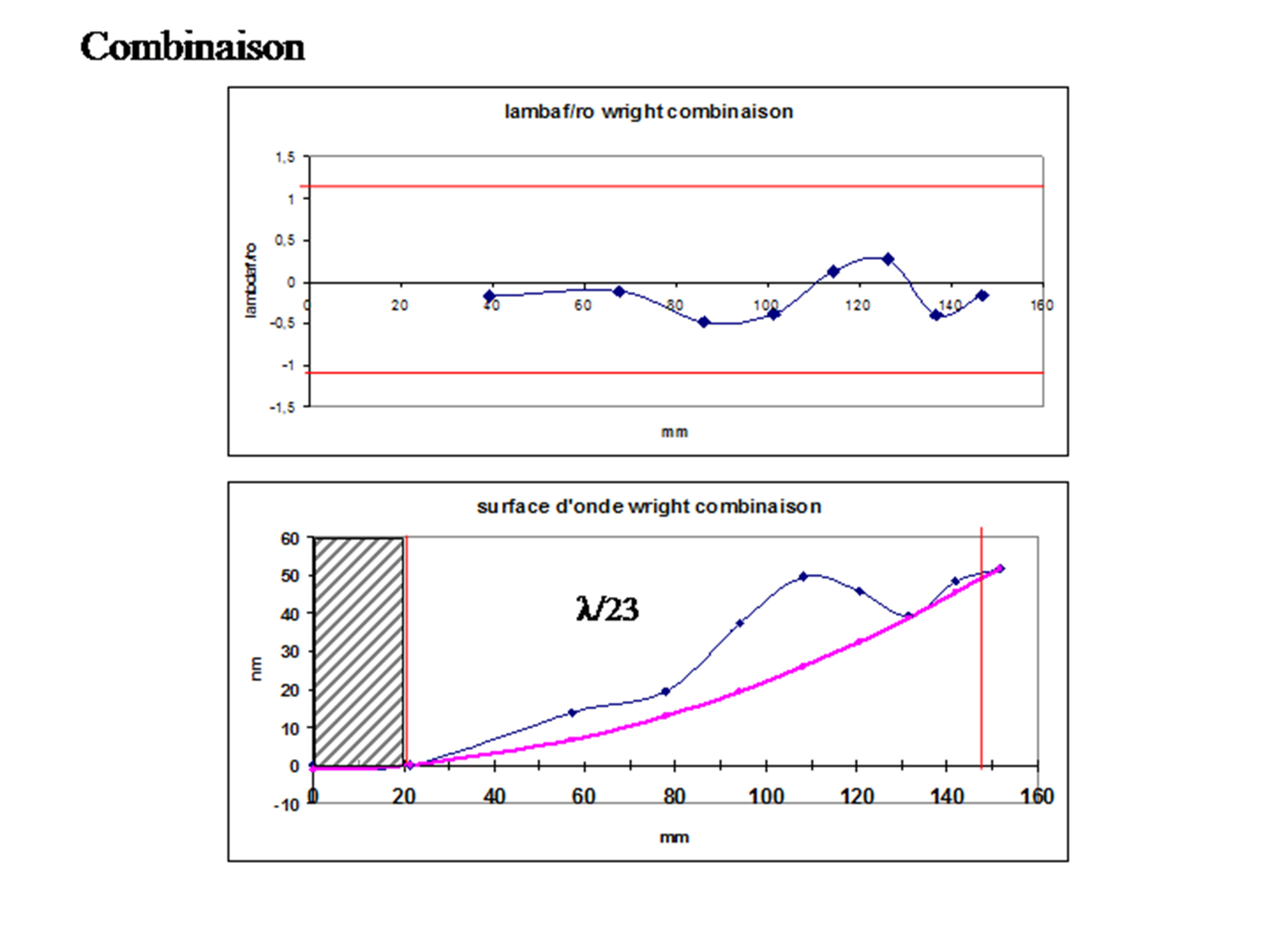
La lame présente un léger bord relevé pour corriger le miroir cf figure de gauche ci dessus. La combinaison calculée pour un simple passage est mesurée à Lambda/23 avec un coefficient de déformation de -1, cette précision est sans doute illusoire. Mais sauf astigmatisme important la combinaison complète a des chances d'être à lambda /10 avec le secondaire à lambda/15. Avant l'aluminure je contrôlerais la combinaison sur la polaire, pour cela je doit réaliser le tube.
Réalisation du barillet:
Le barillet est composé de 6 points sur la périphérie et d'un point central comme expliqué précédemment. 3 des points sur la périphérie et le point central sont constitués de levier astatiques
la douille de 8mm de diamètre qui appuis sur le miroir est en inox qui coulisse dans un palier en bronze. une bille en delrin sert de point d'appuis sur le dos du miroir. Les leviers sont représentés ci dessous. La masse en bronze est réglable sur une tige fileté, tige qui sert également pour bloquer la tête du levier sur l'axe de rotation. L'axe de rotation également en inox tourne sur des paliers standards muni de roulements à rotules.
Le fond du tube est en CP de bouleau de 18mm d'épaisseur. Les appuis latéraux sont des cages de roulement
4 douilles supplémentaires à 90°sont prévues pour éliminer un astigmatisme résiduel si nécessaire
Le miroir secondaire de 46mm de diamètre à lambda/15 sur l'onde (antares optics) est porté par la lame. Pour éviter de percer la lame le porte secondaire sera collé sur la lame .
Le support du secondaire est composé d'une pièce en acier (coefficient de dilatation plus faible que l'aluminium) collée sur la lame, d'un tube et du système comportant les 3 vis de réglage M5 du secondaire. Le support du secondaire est coupé à 45° et le miroir est tenu par un manchon en laiton de quelques 10ieme de mm d'épaisseur qui vient se positionner sur le support à 45°.
Le miroir peut être réglé en hauteur (distance lame secondaire) avec les 3 vis de réglage. Le rappel de la structure est réalisé par un ressort qui vient plaquer le support du miroir contre les 3 vis de réglages.
Le support du miroir secondaire est collé sur la lame pour éviter d'avoir à percer la lame polie.
Un test a été réaliser pour valider la procédure de collage. Le collage est réalisé avec une colle époxy 3M DP190. La colle est mélangée à 5% de billes en verre de 100µm pour assurer un collage uniforme.
Le collage est très résistant et pratiquement indémontable même après chauffage sous air à 250°C. La pièce en acier a été centrée sur la lame au moyen d'un masque
Résultat du collage sur la lame.
La lame installée dans son barillet avec le miroir secondaire.
Le barillet supportant la lame est en bois (CP de bouleau) avec des anneaux en plexiglas noir pour supporter la lame et l'immobilisée dans son logement. Le barillet est fixé sur le corps du tubes par 3 vis tirants et 3 vis poussant ce qui permet de régler l'inclinaison de la lame pour éviter les reflets parasites.
La lame porte dans son barillet sur 6 patins souples en feutre pour éviter les déformations et sur 3 points latéraux.
Réalisation du tube
Le tube est en CP marine de 5mm d'épaisseur , 4 diaphragmes sont installés dans le tube pour éviter les réflexions parasites des parois. Pour régler le miroir secondaire une trappe est ménagée sur une des faces du tube pour accéder aux vis de réglage du secondaire.
diaphragmes installés dans le tube
Pour minimiser l'obstruction centrale, le porte oculaire est un porte oculaire avec un profil bas et il est installé en retrait par rapport à la surface du tube. Il est positionné pour éviter l'obstruction du faisceau. Les dimensions du tube sont de 360*360 mm, la forme carré permet d'avoir un volume interne important par rapport au diamètre du miroir.
Un prolongateur léger de 36cm est positionné au bout du tube pour éviter la condensation sur la lame, le prolongateur et le barillet seront chauffés pour éviter la condensation sur la lame.
Porte oculaire renfoncé dans la parois du tube le tube avec le baffle au dessus de la lame
L'ouverture ménagée dans la parois pour régler le secondaire
Modification de l'abri du télescope de 500mm
Je pense installer ce tube de télescope sur mon T500 actuel. Pour cela je doit modifier l' abri en surélevant le toit pour que l'ensemble du télescope puisse passer par l'ouverture de l'abri qui recule.
l'ancien toit est démonté avec l'aide d'un ami (Maurice Wierczynski)

puis la charpente est démontée et les piliers de la structure sont prolongés de 40cm
La charpente est remise en place (non sans mal)
La toiture est refaite:
on voit bien les 40cm gagnés en hauteur
Les lambris constituant les parois sont remplacés:
L'abri est opérationnel pour accueillir le nouveau tube fixé sur le T500mm:
La position du tube permet de conserver le pointage du télescope vers le pole. Le rééquilibrage du télescope a nécessité le déplacement et le rajout de contrepoids.
Première lumière:
PSF epsilon lyre: Légère dissymétrie du premier anneau (à améliorer)

diamètre du premier minima 0.94"
Ciel profond:
essais malgré le miroir secondaire qui couvre un champ très limité et qui participe à l'allongement des étoiles dans les coins
poses rapides unitaires 5s pose totale 480s (problème de tilt du plan focal)
poses rapides unitaires 0.5s pose totale 240s
Jupiter avec une turbulence assez forte et un échantillonnage trop faible :


29-07-2021 00h18 IR685nm 29-07-2021 00h50 IR685nm

29-07-2021 01h20 I R685nm la résolution est de l'ordre de 0.62" (résolution théorique 0.55")

2021-09-05 22:50:18 Omega1 269.3° Omega2 307.9° Omega3 135.9° Diam 48.6" la
résolution est proche de 0.55"




Cliquer sur les images pour les agrandir
© Jean DIJON : Tous les documents présents
sur ce site sont protégés par les lois sur les droits d'auteur.
La reproduction et la diffusion de ces documents sont interdites sans le consentement de l'auteur.