"Telescope Backer Schmidt entierement corrigé avec un champ plan"

Cette combinaison type Schmidt Cassegrain (cf. figure 1) est très intéressante et somme toute plus facile à réaliser qu'un Schmidt avec doublet (on doit tailler un miroir secondaire à la place du doublet). La qualité des images limité par le sphéro chromatisme de la lame conduit à des taches focales de 10µm dans tout le champ pour un spectre allant de 0.4 à 0.8µm et pour une ouverture de 3. C'est équivalent au schmidt. Pour un système plus ouvert, la qualité se dégrade à cause du chromatisme et la solution Schmidt avec doublet est meilleure. Le primaire très ouvert est pratiquement sphérique ou complètement sphérique suivant la solution retenue. L'obstruction centrale est comprise entre 0.4 et 0.5 suivant le champ couvert. C'est important mais il s’agit d'un télescope photographique. Le champ peut être considérable (limité par l'obstruction) car les aberrations du 3ieme ordre sont toutes corrigées et le champ est plan.

1) Les trois solutions possibles

2) Performances optiques

2.1 Baker type B

2.2 Baker type C

2.3 Slevogt

3) Modification d'un Schmidt argentique

3.1 étude optique

3.2 réalisation du secondaire

4) Méthode de réalisation de la lame par dépression

4.1 calcul de la dépression et du rayon de courbure de l'outil

4.2 réalisation de la casserole et de la lame

4.3 conseils pratiques pour la réalisation de la lame

1) Les 3 solutions possibles

Baker_type B : le primaire est très légèrement aspherisé et le secondaire est sphérique.

Le secondaire peut être taillé dans l'outil qui a servi à doucir le primaire et il est contrôlé par interférences sur le primaire avant asphérisation. La suite des opérations de taille des miroirs est la suivante:

On taille le miroir avec son outil en verre (on part de glace de St Gobain de 19mm d'épaisseur en protégeant la face arrière que l'on garde polie pour le contrôle interférentiel)

On poli le primaire sphérique avec un outil en plâtre recouvert de poix (contrôle au Foucault)

On découpe le secondaire dans l'outil on le poli avec un outil en plâtre

On contrôle le secondaire sur le primaire (interférences)

On contrôle la lame sur le primaire (Foucault)

On aspherise le primaire (Foucault)

Le primaire peut être percé pour rendre le foyer accessible et loger la camera CCD par exemple cela dépends de la combinaison choisie et n'est pas obligatoire.

Baker_type C : le primaire est sphérique le secondaire est légèrement asphérique

Cette solution est aussi bonne optiquement que la solution B il faut aspheriser le secondaire (¼ d'un Cassegrain)

On taille le miroir avec son outil en verre (on part de glace de St Gobain de 19mm en protégeant la face arrière que l'on garde polie pour le contrôle interférentiel)

On poli le primaire sphérique avec un outil en plâtre (contrôle au Foucault)

On découpe le secondaire dans l'outil on le poli avec un outil en plâtre

On aspherise le secondaire contrôle du secondaire sur le primaire (interférences)

On contrôle la lame sur le primaire (Foucault)

_Slevogt : les deux miroirs sont sphériques ce qui introduit un léger astigmatisme qui n'est pas gênant jusqu'à 1° de demi champ au moins. C’est la solution si on ne veut pas aspheriser un des miroirs (la faible asphérisation d’un des miroir n’est pas un gros travail)

La distance lame miroir est de l'ordre de 1.4f contre 2f pour un Schmidt la combinaison est donc plus compacte.

La lame peut être taillée dans de la glace de St Gobain à défaut de BK7 plus transparent. On rends légèrement sphérique la première face pour limiter le chromatisme et on aspherise la deuxième par la méthode des poissons par exemple ou par la méthode de dépression sous vide dans ce dernier cas on part d'un verre plus mince et on aspherise les deux faces. La déformation est environs 2.5 fois la déformation du Schmidt équivalent mais compte tenu de l'ouverture cela reste raisonnable.

2) Performances optiques

Le schéma optique du système est représenté figure1 on vas comparer les trois combinaisons ouvertes à F/D=3

2.1 BAKER TYPE B F/D=3 SECONDAIRE SPHÉRIQUE

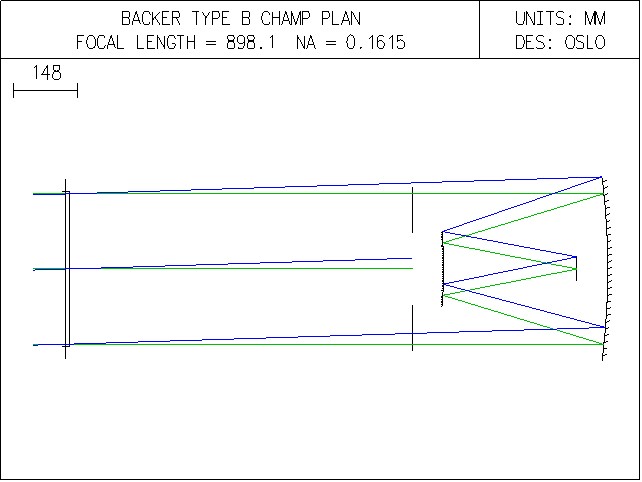
Figure 1 schéma optique du télescope Baker

BAKER TYPE B CHAMP PLAN:

SRF rayon épaisseur ½ ouverture verre NOTE

1 80000 10.0 150.0 Asphérique BK7 C *

2 infini 1246.0 150.0 AIR

4 -1170 -380.5 176.6 miroir asphérique

5 -1170 -- 71.3 miroir

Image infini 309.15 23.5 plan focal diamètre 47mm

*CONIC AND POLYNOMIAL ASPHERIC DATA

SRF Cv AD AE

1 1/80000 -2.0283e-10 -1.6038e-16

4 0.016 PRIMAIRE bs1=0.016

Données optique Baker B

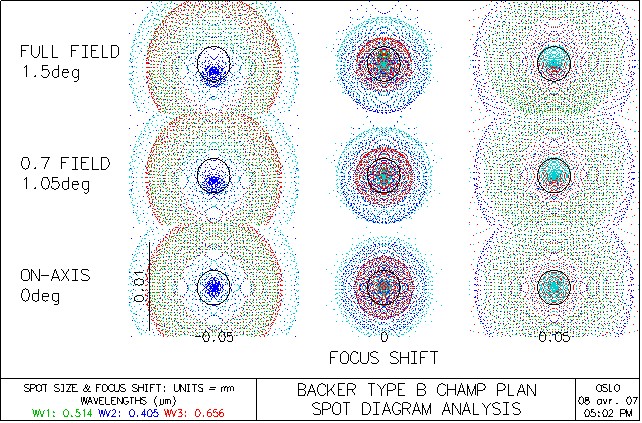
SPOT Diagramme LAMBDA 0.4 0.8 µm:IMAGES DE 10µm DANS TOUT LE CHAMP

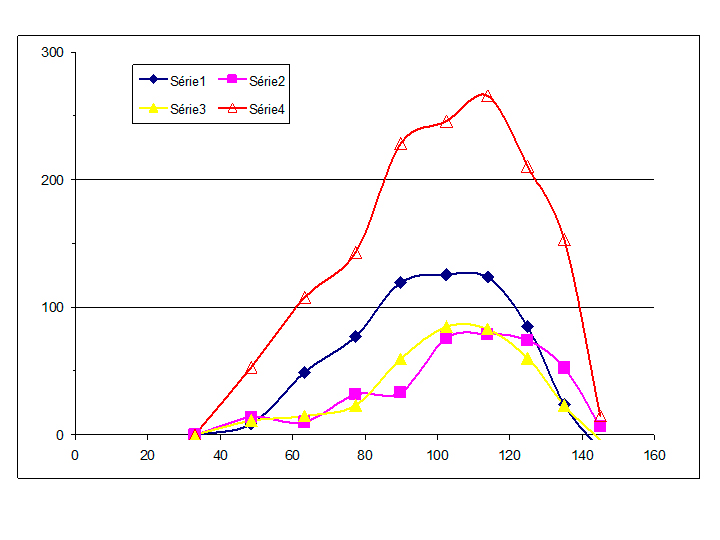
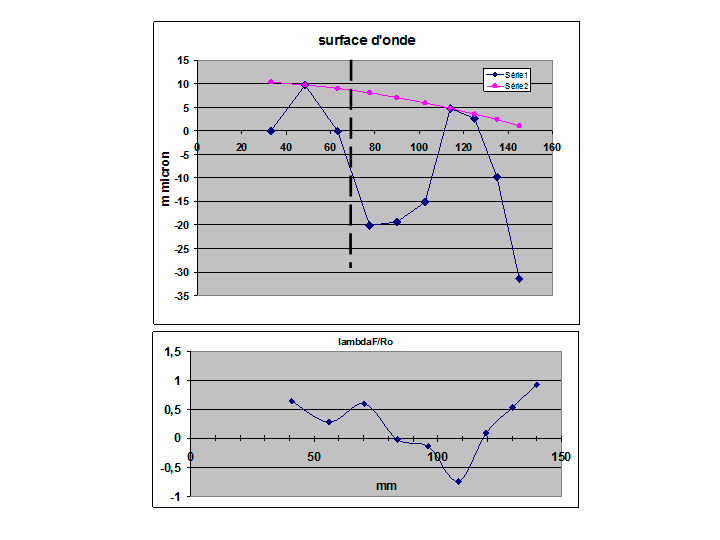
Le télescope est limité par la diffraction autour de la raie verte du mercure. Le sphero chromatisme de la lame empêche d'avoir une meilleure correction sur tout le spectre.

La forme de la lame est donnée ci-dessous :

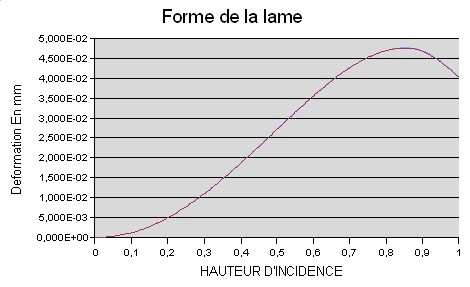
Son équation est 0.5 Cv r^2+Ad r^4+Ae r^6 avec Cv=1/80000 Ad=-2.028E-10 Ae=-1.6E-16

Elle est indiscernable (cf. figure ci dessus) de l'équation 2.485 A (ρ^4-1.44ρ^2) ou

ρ=2r/D

A=1/(512 (n-1)) (D^4)/(F^3)

F est la focale résultante du télescope ici F=898mm

On peu tester la lame contre le primaire sphérique (f=585mm) l'aberration théorique est (double passage à travers la lame) x=2*2.485*(h^2)/2F ce qui permet le contrôle de la lame au Foucault

On peut également rendre la face 2 sphérique et déformer la face 1 qui reste plane (méthode de taille des poissons) dans ces conditions les paramètres de la lame sont:

Face 1: plane déformation 0.5Cv r^2+Ad r^4+Ae r^6 avec Cv=1/115000 Ad=-2.028E-10 Ae=-1.6E-16 soit 2.5 A (ρ^4-ρ^2)

Face 2: sphérique convexe R=26000mm

2.2 BACKER TYPE C: PRIMAIRE SPHERIQUE

BACKER TYPE C CHAMP PLAN

SRF Rayon épaisseur ½ ouverture verre NOTE

AST 80000 10.0 145.0 BK7 LAME

2 -- 1263.0 145.0 AIR

4 -1170 -380.5 175.0 miroir PRIMAIRE

5 -1170 0 71.5 miroir SECONDAIRE

IMS -- 309.157 23.5 *

*CONIC AND POLYNOMIAL ASPHERIC DATA

SRF Cv AD AE

1 1/80000 -1.9950e-10 -1.5300e-16 LAME

5 -0.25 SECONDAIRE bs2=-0.25

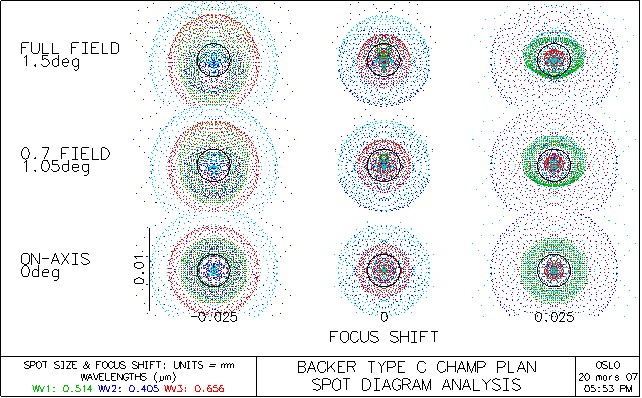
spot diagramme solution C : les images font 10µm dans un champ qui peut être largement supérieur à 1.5° équivalent à la solution B

Cette solution est complètement équivalente à la solution B avec une distance légèrement supérieure de la lame. Il est sans doute plus facile de laisser le primaire sphérique on peut transformer un ancien Schmidt argentique de cette façon.

2.3 SLEVOG les deux miroirs sphériques

SLEVOG MIROIRS SPHERIQUES

SRF Rayon épaisseur ½ ouverture verre NOTE

AST 80000 10.0 150.0 BK7 C *

2 -- 1276.0 150.0 AIR

4 -1170 -380.5 177.0 miroir

5 -1170 -- 71.6 miroir

IMS -- 309.082077 23.5 plan focal

*CONIC AND POLYNOMIAL ASPHERIC DATA

SRF Cv AD AE

1 1/80000 -1.9800e-10 -1.5200e-16 lame

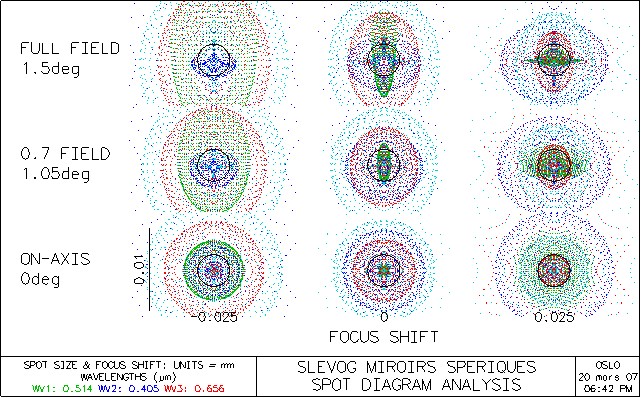
spot diagramme slevogt: à cause de l'astigmatisme les images sont un peu moins bonnes en bord de champ que les solutions B et C

Cette solution avec deux miroirs sphériques est très intéressante , l'astigmatisme n'est pas gênant jusqu' à 1° ou 1.5° de l'axe. Néanmoins pour un amateur une fois que les miroirs sont sphériques le travail d'asphérisation du secondaire n'est pas grand chose aussi je pense que la solution C est la plus intéressante à réaliser. La table ci dessous récapitule les caractéristiques optiques des 3 combinaisons

	BACKER B	BACKER C	SLEVOG
PRIMAIRE R=1170	bs1=0.016	bs1=0	bs1=0
SECONDAIRE R=1170	bs2=0	bs2= -0.25	bs2=0
DISTANCE LAME PRIMAIRE	1246	1263	1276
Option 1 lame: Taille poissons
FACE1 plane déformée Cv	1/115000	1/115000	1/115000
FACE2 sphérique convexe	R2=260000	R2=260000	R2=260000
Option 2 lame: Taille par dépression
FACE1 sphérique déformée Cv	1/80000	1/80000	1/80000
FACE2 plane
Ad*1E10	-2.028	-1.995	-1.98
Ae*1E16	-1.60	-1.53	-1.52
TEST lame: aberration longitudinale	22,4287(h^2)/2F	22,3892(h^2)/2F	22,3712(h^2)/2F
Focale résultante mm	898	898	898

Caractéristiques optiques des 3 solutions ouvertes à F/D=3 F=898mm

Deux options pour la lame sont données (les coefficients de déformations sont les mêmes pour les deux options)

RAYON CHAMP PLEINE LUMIERE	0.8°	1°	1.5°
DIAMETRE SECONDAIRE focale 900mm	125mm	130mm	145mm
DIAMETRE CHAMP	25mm	31mm	47mm
OBSTRUCTION LAME 300mm	0.42	0.43	0.48

Diamètre du secondaire en fonction du champ de pleine lumière couvert

3) MODIFICATION D'UN SCHMIDT argentique 220/310/718

Ce télescope F/D=3.3 réalisé dans les années 80 n'est plus en service depuis la disparition du 2415 aussi j'ai décidé de le modifier en Baker Schmidt pour pouvoir y adjoindre une camera CCD. Des pièces optiques je ne conserve que le primaire sphérique qui représente un gros travail d'ébauchage, il faut donc retailler une lame et le secondaire. Pour conserver un rapport d'ouverture équivalent (ce qui permet de poser plus longtemps dans des sites de qualité médiocre et d'atteindre une magnitude limite plus élevée) la lame sera portée à 290mm utile et le champ de pleine lumière à 2.5° de diamètre. Ce champ pourra évoluer ultérieurement vers un champ plus grand en fonction des futures camera CCD.

3.1 Étude optique

La distance entre le primaire et le secondaire est de 504mm

La distance secondaire foyer est de 301mm il reste donc plus de 20cm pour caser la camera CCD entre le foyer et le primaire. Le primaire peut donc rester en l'état sans perçage ce qui nécessiterai de le surfacer à nouveau.

La distance lame primaire est de 1518mm

Le diamètre du secondaire est de 130mm ce qui donne une obstruction de 45%

Le coefficient de déformation du secondaire est de -0.37 ce qui est faible, comme le primaire est aluminé, le secondaire sera contrôlé sur l'outil servant à le réaliser qui servira de calibre

La focale résultante du système est de 1022mm soit un rapport d'ouverture de 3.5

BACKER TYPE C CHAMP PLAN

surface rayon épaisseur ouverture (rayon) verre

1 150000 10.0 150.0 A BK7

2 -- 1518.0 150.0 AIR

4 -1436 -504.0 155.0 miroir concave (sphérique)

6 -1436 -- 63.6 miroir convexe (asphérique)

image -- 301.24 22.3 *

Données surfaces asphériques

SRF Cv AD AE

1 1/150000 -1.20 e-10 -6.90e-17 DEFORMATION LAME

6 -0.370 DEFORMATION DU SECONDAIRE

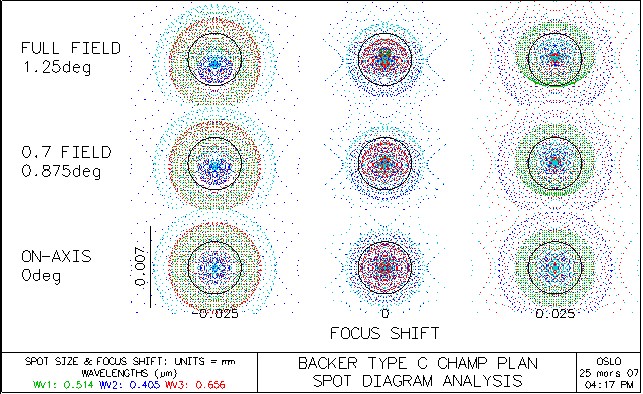
Spot diagramme: le télescope est pratiquement limité par la diffraction dans tout le champ entre 0.4µm et 0.9µm on peut utiliser des capteurs CCD avec des pixels de 4 à 5µm

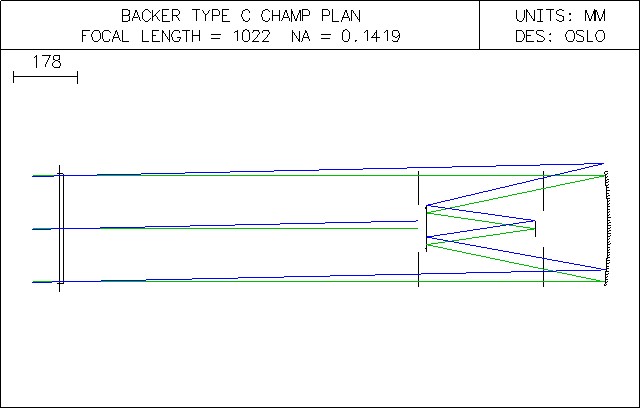
Système optique

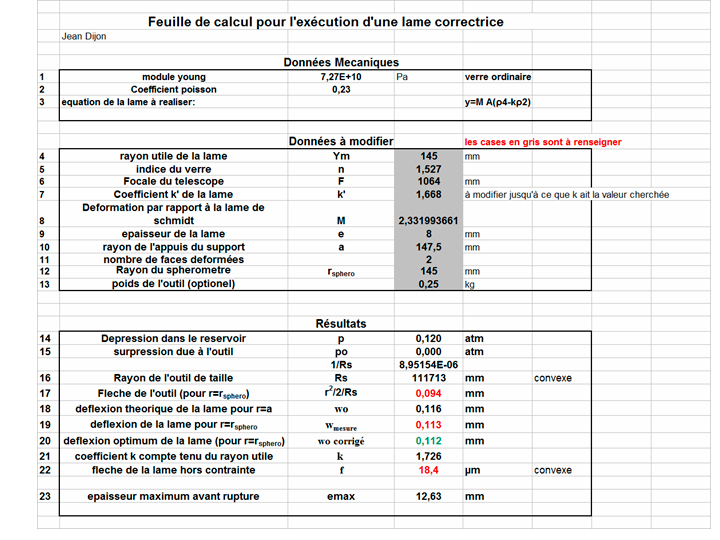
La définition optique d'un tel système (forme de la lame, coefficients de déformation des miroirs) peut se faire entièrement avec la dioptrique du troisième ordre. Une feuille de calcul permettant de déterminer les paramètres du télescope se trouve ici.

l'équation de la lame à réaliser est 2,118*A*(ρ⁴-1.32ρ²)

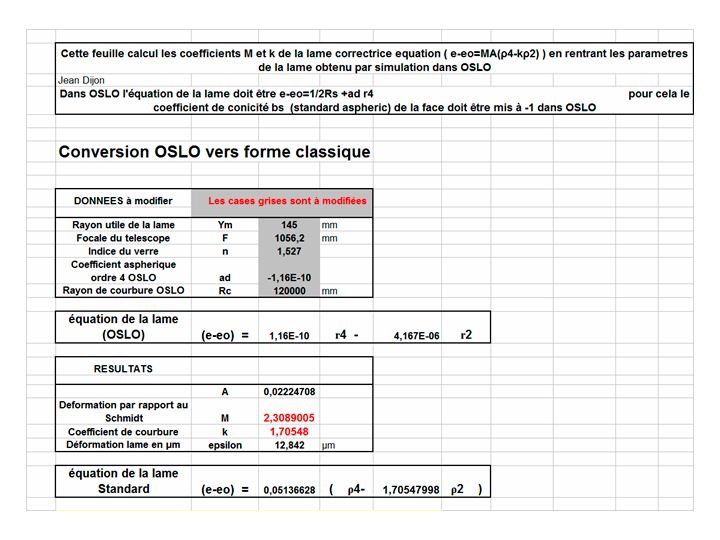
Sinon on peut utiliser ©OSLO (version étudiante ) http://www.lambdares.com/oslo-university-program

3.2 Réalisation du Miroir secondaire sur calibre interférentiel

Le miroir secondaire est taillé dans de la glace de St Gobain épaisseur 15mm. L'outil concave servant à l'ébauchage sera poli sphérique pour réaliser le calibre interférentiel permettant de contrôler le miroir convexe.

Dans notre cas nous sommes partis de disques d'un diamètre de 140mm

-Les deux disques ont étés ébauchés et doucis l'un sur l'autre comme nous voulons réaliser un rayon de courbure précis celui ci est contrôlé au sphéromètre.

3.2.1 réalisation d'un sphéromètre économique

On peut réaliser un sphéromètre à partir d'une butée micrométrique insérée dans une planche en aggloméré les trois pieds étant réalisés à partir d'une tige fileté de 6 ou 8 mm.

On réalise soit des pieds coniques soient des pieds avec une bille de roulement de rayon r_bille collée à l'araldite

On commence par régler la perpendicularité de la butée en posant le système sur un morceau de glace de St Gobain et on règle la hauteur des 3 pieds pour que le reflet de la butée et la butée soient parallèles.

On rode légèrement les pieds sur un plan s'ils sont coniques (verre doucis avec de l'émeri 40mn)

Il reste à étalonner les rayons intérieur et extérieur de porté du sphéromètre en effet ces deux rayons ne sont pas identiques

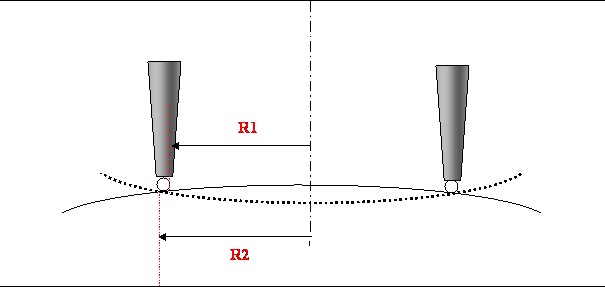
Si les pieds sont terminés par des billes on a:

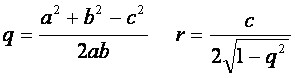
avec a,b,c les distances entre les centres des pieds pris deux à deux. Pour les mesurer, on prends un pieds à coulisse et on mesure les distances extérieures A,B,C incluant les billes. On retranche le diamètre des billes à ces valeurs. On a doc a=A_dbille, b=B-dbille, c=C-dbille

On a alors si h est la flèche de la surface mesurée en prenant une référence de hauteur sur un plan ( qui faute de mieux peut être de la glace de St Gobain)

Pour une surface concave:

R_concave=(r²+h²)/2h+d_bille/2

Pour une surface convexe:

R_convexe=(r²+h²)/2h-d_bille/2

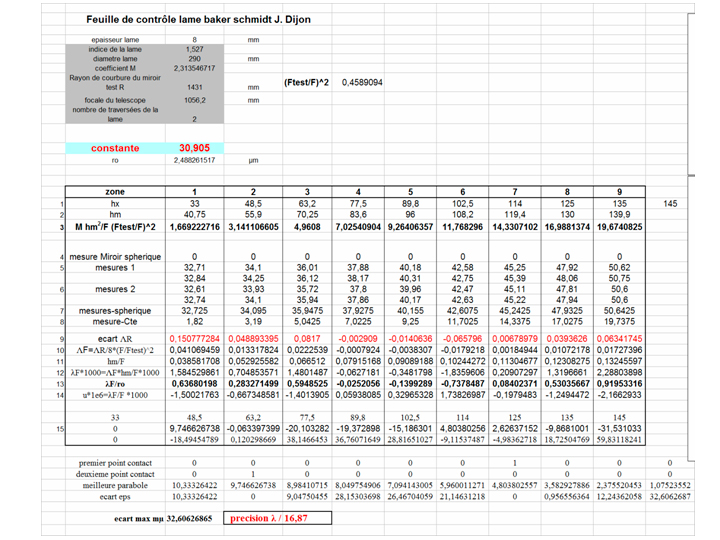
3.2.2 Polissage réalisation du calibre

Lorsque les deux miroirs sont doucis on réalise des outils en béton (sable tamisé et ciment) que l'on coule sur les miroirs. On protége la surface du miroir avec un film alimentaire bien tendu et on enroule sur la tranche du miroir du papier fort pour faire le moule l'épaisseur à donner à l'outil est de 15 à 20mm. On réalise cette opération sur chaque miroir pour obtenir un outil concave et un outil convexe. Après une semaine de séchage on démoule et on peint les outils. L'intérêt du béton par rapport au plâtre est qu'il ne craint pas l'humidité.

On réalise alors sur chaque outil un polissoir par collage de carrés de poix ou par coulage directe et rainurage si les miroirs sont tout petits.

Les deux outils concave convexe plus le calibre et le miroir en cours de réalisation

3.2.3 Observation des interférences

Pour observer les interférences entre les deux surfaces j'ai utilisé un montage très simple à savoir un petit tube néon du commerce qui est disposé sur un diaphragme pour limiter l'étendue de la source. Le tube est placé au centre de courbure du calibre (concave) et l'image est photographiée au moyen d'un appareil photos numérique disposé sur un pied. le miroir et le calibre reposent sur un statif en bois isole du sol et les miroirs repose sur ce statif avec l'interposition d'un tissus épais pour éviter les contraintes. Le système est très sensible.

Miroir sur son calibre avec 3 cales en papier à 120° pour réaliser le coin d'air on pose le calibre sur un molleton pour éviter les contraintes

Image d'interférences obtenues à partir d'un tube néon. A gauche en lumière totale à droite la couche bleu de la photo qui sert a faire les mesures. Le miroir présente un trou central de lambda/4

la courbure d'ensemble est identique à celle du calibre. Le reflet est celui du tube néon diaphragmé

Le calibre est réalisé avec le coefficient de déformation du secondaire ce qui permet un contrôle du secondaire plus aisé. on cherche à obtenir des franges droites entre le secondaire et le calibre. On cherche une précision de l'ordre de lambda sur 4 sur l'onde.

4 ) Méthodes de RÉALISATION DE LA LAME par dépression

Cette technique est la plus facile à mettre en oeuvre si l'on possède une pompe permettant la réalisation d'un vide primaire assez peu poussé il s'agit en fait de réaliser une dépression de l'ordre de 0.2 atmosphère. On réalise un support permettant d'assurer la dépression de la lame ce support qui est adapté à la lame et facilement interchangeable. Le support est fixé à un réservoir connecté à la pompe au moyen d'un robinet étanche ce qui permet après pompage du système de travailler la lame et son support comme une seule pièce déconnectée de la pompe.

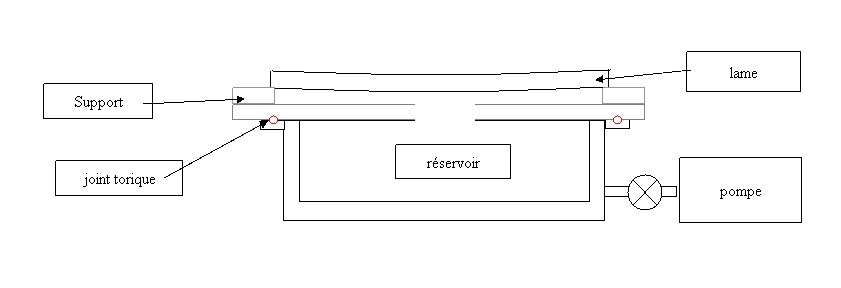
La lame en appuis sur le support se déforme sous l'influence de la différence de pression entre le support et l'extérieur. On taille la surface de la lame sous contrainte en forme de sphère. Une fois la lame dé contrainte, elle prends la forme voulue si la pression dans le réservoir et le rayon de la sphère ont les valeurs adaptées que nous allons calculer.

4.1 Calcul de la pression du réservoir et du rayon de l'outil de taille.

L'équation de la lame à réaliser s'écrit d'une façon générale (e-eo)= MA(ρ⁴-kρ²) = MA/Ym⁴ (y⁴-kYm²y²)

avec

ρ = y/Ym hauteur d’incidence normalisée (varie entre 0 et 1 au bord)

A= 1/32/(n-1) Ym⁴/F³

^{D=2Ym est le
diamètre de la lame}

^{F est la focale du
télescope}

si M=1 il s'agit d'une lame de Schmidt

Pour une lame dont le profil a été calculé dans OSLO on dispose de deux paramètres: le rayon de courbure Rc de la lame et son coefficient de déformation ad on a :

(e-eo) = (1/2R_c) y²+ad y⁴

ce qui permet de calculer M et k

M=32ad(n-1)F³

k = -1/(2ad R_cYm²)

L’équation de la lame à réaliser dans notre cas est 2,118*A*(ρ⁴-1.32ρ²)

avec D=290mm n=1.52 F=1022mm

On peut tailler cette lame par dépression [5] [6]

La fleche w d'une lame soumise à une pression p et supportée sur un diamètre de 2a est

w=(3p(1-s)/(16Ee³))*((6+2s)a²r²-(1+s)r⁴) (1)

avec E module de Young du verre

s coefficient de poisson du verre

e épaisseur de la lame

cette forme est proche d'une sphère de rayon Rs dont la déflexion est

ws=r²/2Rs (2)

lorsque la lame est taillée avec cette sphère de référence l'épaisseur de verre enlever vaut:

h=w-ws=[3a²p(1-s)(3+s)/(8Ee³)-(1/2Rs)]r²-[3p(1-s²)/(16Ee³)]r⁴ (3)

ce qui est précisément l'équation cherchée de la lame. Dans notre cas particulier on a

h=2,118*(1/(32(n-1)F³))*(r⁴-1.32a²(Ym²/a²)r²)

Les deux faces sont à surfacer on a donc pour chaque face la déformation suivante (moitié):

h=1,059*(1/(32(n-1)F³))*(r⁴-1.32a²(Ym²/a²)r²)

Avec a=145mm et F=1022mm

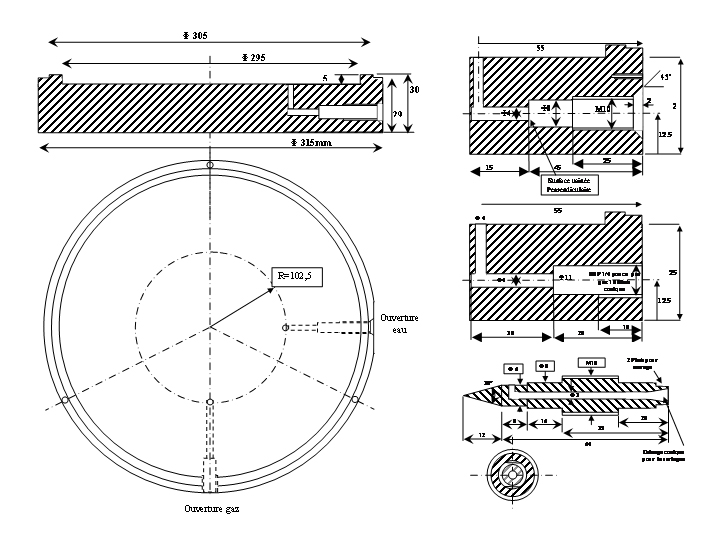
On part d'une lame de 310mm pour avoir 10mm de garde tout le tour, un rayon d'appuis de a=150mm (cf figure ci dessous) et une lame finie de 290mm. Dans ce cas on doit avoir pour conserver la même forme utile un coefficient pour la lame complète k'=kYm²/a²:

1.32*145^2=k'*150^2 d'ou le coefficient en r² à réaliser k'=1.215

La pression à appliquer est obtenue en égalisant les termes de degré 4 soit :

p=MEe³/ (6(n-1)F³(1-s²)) (4)

le module d'Young du verre vaut E= 72,7 10⁹ pa

le module de poisson s= 0,23

n=1.52

M=1.059

F=1022mm

e=10mm

On trouve p=2,410⁴ pa = 0,24 atm c'est la dépression à appliquer au réservoir.

Le rayon de courbure de l'outil de taille est obtenu en égalant les termes en r²on a:

1/Rs=a²M/(16(n-1)F³)*(2(3+s)/(1+s)) (5)

pour M=0.5 et k'=1.5 (lame de Schmidt déformée sur les deux faces) on retrouve bien la formule donnée dans [5]

ce qui donne dans notre cas pour chaque face avec a=150mm

M=1.058

F=1022mm

k'=1.215

s=0.23

Rs=91760mm

On règle la pression au moyen de la déflexion au centre de la lame ce qui permet de s'affranchir des erreurs sur les coefficients mécanique de la lame (épaisseur module d'young) ainsi que de la nécessite de mesurer précisément la pression. Cette déflexion vaut

wo=3a⁴p(1-s)(5+s)/16Ee³=Ma⁴/(32F³(n-1)) (5+s)/(1+s) (6)

soit dans le cas présent: wo=0,129mm

La contrainte maximum de tension T d'une lame d'épaisseur e soumise à la pression p s'écrit:

en remplaçant p par l'expression (4) on obtient T=(3+s)KEea²/(16(n-1)(1-s²)F³)

Cette tension doit être inférieure à la tension de rupture Tmax de la lame donc e < Tmax 16(n-1)(1-s2)/(E(3+s)) F³/Ka²

On a pour une face finement doucie mise en tension une limite de rupture de 7.8 10⁷ pa donc l'épaisseur de la lame doit être inférieure a

On voit qu'en partant d'une lame de 10mm on est encore loin de la limite de rupture.

La feuille de calcul 2 permettant de calculer la pression et la forme de l'outil lorsque l'équation de la lame à réaliser est connue se trouve ici

On renseigne les cases en gris et on a l'ensemble des résultats lignes 14 à 22

La feuille de calcul 1 permettant de mettre l'équation sous la forme nécessaire pour l'utilisation de la feuille de calcul 2 lorsque le calcul de la lame a été faite dans OSLO se trouve [ICI]

La casserole figure ci dessous est une pièce très plate qui ménage sous la lame un faible volume qui sera pompé. L’épaisseur totale est assez importante 25 à 30mm pour éviter les déformations de la casserole lors de la mise sous vide. Un point critique auquel il faut apporter un soin particulier est la qualité de l’appui sur lequel repose la lame. Toute erreur à ce niveau se répercutera sur la forme d’ensemble pouvant générer rapidement de l’astigmatisme donc après usinage ce rebord sera rodé soigneusement avec de l’émeri 40mn et 60mn contre un outil en verre. Le fond de la cavité sera éventuellement peint en noir pour facilité l’observation de la lame en cours de polissage [18]. Passons aux divers moyens pour faire le vide. On peut soit pomper l’air contenu dans l’enceinte soit remplir la casserole d’eau et pomper le volume nécessaire avec une seringue pour obtenir la bonne dépression [19]. Cette dernière méthode procure un assemblage rigide lame casserole et minimise les problèmes de déformation de la lame lors de son travail.

Pour pomper l’air le moyen le plus compliqué est d’utiliser une pompe à vide électrique. En effet on veut pouvoir régler finement le vide à l’intérieur de la casserole et si on branche directement la pompe sur cette dernière même à travers un robinet compte tenu du vide limite de la pompe on risque de faire exploser la lame. Il faut donc pomper dans un premier temps un réservoir intermédiaire l’isoler et vider la casserole avec ce réservoir. On peut par contre utiliser des moyens beaucoup plus économiques de laboratoire de chimie pour réaliser ce vide partiel. Une trompe à eau qui coûte quelques dizaines d’euros [20] permet d’atteindre des vides largement suffisants. On fixe la trompe sur un robinet d’eau ayant un bon débit et on raccorde l’orifice de pompage soit à un réservoir soit directement à la casserole à travers un robinet étanche au vide. La troisième possibilité est d’utiliser une petite pompe à main. Celle que j’utilise provient d’un ancien système d’hypersensibilisation. L’étanchéité entre la casserole et la lame est réalisée avec de la graisse à vide [20] ou faute de mieux avec de la graisse épaisse propre ou de la vaseline. On centre soigneusement la lame sur son support (pions de centrages) et on fait le vide. La flèche induite par la dépression est mesurée avec un sphéromètre que l’on réalise spécialement et qui porte sur le bord de la lame. On utilise l’équation (6) pour connaître la flèche à atteindre. Le zéro du sphéromètre est fait sur un marbre ou mieux sur un plan que l'on peut réaliser avec de la glace de Saint Gobain en utilisant le rodage classique de 3 surfaces les une sur les autres.

Avec de l’eau, le montage adapté de [19] comporte un pointeau (figure ci dessous) qui est relié à la seringue de pompage et qui permet par serrage d’isoler le volume de la casserole. Le volume de liquide à pomper qui dimensionne la taille de la seringue est donné par :

Typiquement il fait environ 5ml pour une lame de 300mm. On peut régler précisément la déflexion au micron près avec une seringue graduée à 0,1ml. On utilise de l’eau distillée pour éviter tout risque d’attaque de la surface du verre par le contact prolongé avec l’eau et on la dégaze au maximum en la faisant bouillir. On rempli la cavité et on pose la lame sur la casserole. L’opération délicate consiste à faire disparaître la bulle résiduelle entre le verre et l’eau. On presse alors fortement sur le dessus de la lame et on pompe avec la seringue. La flèche est réglée avec le sphéromètre comme dans le cas du gaz.

Dans tout les cas, on rétabli la flèche qui a tendance à diminuer avec le temps et on attends au moins une journée sa stabilisation avant de commencer le travail. Pour améliorer l’étanchéité on réalise si nécessaire un joins démontable entre la casserole et le bord extérieur de la lame avec du silicone.

On doucis la lame déformée avec l’outil n°1 que l’on aura rendu convexe avec le rayon de courbure R_outil(équation 5) sur l’outil n°2. On contrôle ce rayon de courbure avec le sphéromètre qui sert à contrôler la flèche de la lame et qui est suffisamment grand pour porter sur la périphérie de l’outil. Si on a pas de plan étalon on peut utiliser la somme des flèches entre l’outil 1 (convexe) et l’outil 2 (concave) pour déterminer le rayon de courbure moyen entre les deux surfaces. Il faut que les deux surfaces soient bien réunies. On a alors si on utilise un sphéromètre à billes (ayant un diamètre d_bille) portant sur un rayon r

h est la différence de cote entre la surface convexe (prise comme référence) et la surface concave.

Durant le travail de la lame on réuni périodiquement l’outil n°1 sur l’outil n°2 pour préserver sa forme sphérique. On travail à poste fixe normalement avec l’ensemble lame casserole en dessous. Lorsque la lame est finement doucie (avec aucune bulle ne subsistant au centre ) on passe au polissage. A ce stade la flèche de la lame doit être égale à la flèche de l’outil n°1 (cf plus bas).

Donc si on démonte la lame pour la contrôler il faut la remonter en lui imposant une flèche égale à celle de l’outil. Cf explications détaillées plus bas.

On peut utiliser de la poix un peu dure pour réaliser le polissoir (au dos de l’outil n°1 ou sur l'outil n°1) afin de garantir une bonne sphère. Par contre on n’appliquera pas de pression excessive pendant le travail pour éviter de déformer la lame. Le pressage du polissoir se fait en partie sur l’outil n°2 puis on tiédis la poix pour réaliser le pressage final sur la lame. Lorsque le polissage est avancé on casse le vide et on passe à la deuxième face.

On peut contrôler la lame au Foucault pour vérifier si tout a bien marché. Si la déformation n’est pas celle attendue (moitié de la déformation finale) on pourra compenser le problème sur la deuxième face. Avant démontage on repère soigneusement la position de la lame par rapport à la casserole (repères sur la lame et sur la casserole). On remonte la lame sur la casserole deuxième face vers le haut après l’avoir fait tourner dans son plan de 90° par rapport aux repères initiaux. Cette opération permet d’éviter tout problème d’astigmatisme grave induit par le support. On recommence comme précédemment les opérations de polissage sur la deuxième face.

Plan de la casserole pour réaliser la lame. Ici les cotes sont pour une lame de 295mm de diamètre utile. Suivant le principe retenu pour faire le vide (gaz ou eau) on réalise l’un ou l’autre des usinage correspondant voir plans de détails a gauche. Les 3 trous bornes à 120° en périphérie reçoivent des pions de centrage pour maintenir la lame lors de sa mise sous vide. Ils sont enlevés pour tailler la lame lorsque le vide est réalisé. A gauche : détails des usinages de la casserole et du pointeau pour utilisation de l’eau. En haut)

usinages pour la solution eau. au milieu) usinage pour la solution gaz. en bas) détails du pointeau.

J'ai choisi une épaisseur de lame de 8mm ce qui s'est avéré être une erreur car la dépression est faible ce qui conduit à une sensibilité accrue de la déformation avec les variations de pression . La pression atmosphérique en particulier qui varie d'un jour à l'autre et oblige de régler la forme de la lame (la dépression) avant chaque séance. Une épaisseur de 10 ou 12mm aurait été préférable. Mon choix est lié à l'utilisation de verre à vitre ordinaire et je voulais minimiser l'absorption et les déformations induites par les inhomogénéités du verre.

Le premier travail est de roder très soigneusement avec un disque de verre plan le bord de la casserole. J'ai utilisé des émeris 40 et 60mn pour ce travail. Il faut que le bord porte bien uniformément.

Il convient de comprendre comment contrôler les deux pendant la phase de doucissage.

Sans contrainte la lame doit être biconvexe avec une flèche f centre bord mesurée avec le sphéromètre qui vaut

si on déforme les deux faces de la lame (sinon cette flèche est double) cette valeur se trouve ligne 22 de la feuille de calcul

donc sans pression on doit avoir sur chaque face la flèche donnée par (10) lorsque la lame est bonne.

Lorsque l'on met en dépression on prend la référence (le zéro) sur la lame non contrainte puis on règle la flèche à wo (ligne 19 feuille ). On a wo = f + (flèche outil 1) soit ligne 19= ligne 22 + ligne 17

On commence donc par tailler la lame (émeris 2 minutes puis 5minutes et jusqu'au 20mn) biconvexe sphérique, avec une flèche f (ligne 22) de chaque coté, en utilisant l'outil n°2. On en profite par vérifier que la lame est bien d'épaisseur constante (cf. Texereau [3]).

On taille ensuite l'outil n°1 avec l'outil n°2 de façon à obtenir une surface convexe avec une flèche donnée par la ligne 17 de la feuille (ce qui correspond à un outil de rayon de courbure Rs). On s'applique à avoir une surface bien sphérique et doucis avec de l'émeri 5 minutes puis 20mn.

On enduit le bord de la casserole uniformément d'une couche fine de graisse épaisse (sans en mettre une trop grande épaisseur pour éviter que la lame ne glisse) puis on pose la lame sur la graisse, on mesure la cote de la lame fo, puis on pompe et on établit une différence de cote f-fo=wo.

Chaque fois que l'on démonte la lame on refait ce réglage qui assure une déformation correcte à la lame.

J'ai refait ce réglage chaque fois que je commençais le travail à cause des variations de la pression atmosphérique. Si le rodage est correcte on a un joint étanche et on peut travailler sans le réservoir avec juste la casserole sous vide. La flèche fo de la lame non contrainte est contrôlée avec le plan de référence.

Pendant le doucissage, au début il existe une bulle au centre car la lame déformée et l'outil ne sont pas réunis. On fait les séchées lame dessous (casserole dessous). On peut faire quelques séchées casseroles dessus si la flèche f de la lame (rayon de courbure) diminue par rapport à la valeur nominale. Avec le 5mn on réuni les deux surfaces au mieux et on contrôle que la flèche f reste correcte. Une précision de 1 à 2 µm est correcte .Ensuite on passe les émeris jusqu à 60minutes en vérifiant qu'il ne se forme pas une grosse bulle centrale.

Lorsque ce travail est fait, on démonte la lame, on la tourne d'un quart de tour (dans son plan ) pour éviter l'astigmatisme et on taille la deuxième face.

j'ai fait un polissoir classique sur l'outil n°1 avec des carrés de poix de 20mm. Le polissoir est pressé sur l'outil n°2 jusqu'a ce que tous les carrés portent uniformément. puis il est pressé sur la lame. Le polissage a été fait avec de l'oxyde de cérium 3 heures de polissage sur chaque face permettent les premiers contrôles. On poli la lame comme un miroir sphérique.

On peut contrôler la lame sur le primaire sphérique ou sur un autre miroir sphérique.

Le contrôle peut se faire sur le miroir sphérique du télescope ou sur un autre miroir sphérique dont le rayon de courbure R_test =2F_test est différent de celui du télescope.

Si le miroir test a par la plus grande chance la focale F_t du télescope, l'aberration longitudinale au centre de courbure de la lame contre le sphérique est

2 M hm²/2F_t= M hm²/F_t le facteur 2 est liée à la double traversée de la lame et le facteur M est la déformation de la lame par rapport à la lame de Schmidt (cf. paragraphe 4)

Si le miroir test a un rayon de courbure différent de F_t il convient de multiplier cette aberration par (F_test/F_t)² on a donc lors du test une aberration longitudinale théorique

En particulier si on test la lame contre le primaire sphérique du télescope de focale F_prim on a l'aberration longitudinale:

Comme F_prim est plus petit que la focale du télescope à cause du miroir secondaire (Cassegrain) ce facteur (F_test/F_t)²est de l'ordre de 0.5 dans mon cas

L'ensemble des calculs pour établir le bulletin de contrôle de la lame (au foyer du télescope) sont rassemblés sur la feuille de calcul suivante

Les informations concernant le télescope et le miroir test sont rentrés dans les cases grisées

La ligne 3 représente l'aberration longitudinale théorique lors du test (équation 11)

La ligne 4 représente la mesure des zones du miroir sphérique utilisé s'il n'est pas parfait ( le cas échéant on peut utiliser un miroir parabolique )

Lignes 5 6 on trouve les mesures au Foucault et l'aberration de la lame soustraite de l'aberration du miroir ligne 7

Ligne 8 on trouve la ligne 7- la constante de mesure (en rouge) que l'on ajuste au mieux pour minimiser les écarts ΛR (expérience - théorie) ligne 8-ligne3

Ligne 10 on trouve l'aberrations ΛF au foyer du télescope on a ΛF=ΛR/2*(F_t/R_test)²= ΛR/8*(F_t/F_test)²on divise par deux car dans le télescope le faisceau ne traverse la lame qu'une fois et on multiplie par (F_t/R_test)² pour se ramener au foyer du télescope.

ligne 11 on trouve la hauteur d'incidence au foyer du télescope hm/F et non hm/4F (on est au foyer du télescope et non au rayon de courbure) on a ligne 12 l'aberration transversale au foyer du télescope λF=ΛF hm/F

on a ligne 13 l'aberration transversale réduite et ligne 14 la pente de l'onde.

Plus bas on trouve le calcul de la meilleur parabole en définissant les deux points de contact (marqués 1)

Lors des premières mesures on voit si la lame est proche de la forme finale ou si elle est sur corrigée ou sous corrigée. Si elle est sur corrigée on diminue légèrement la pression dans la casserole pour diminuer la flèche de la lame sous contrainte (de quelques µm). On presse l'outil sur la lame avec la nouvelle dépression et on continue le polissage. Si elle est sous corrigée on augmente la flèche en augmentant la pression dans la casserole.

On doit polir complètement les deux faces (on observe par exemple la diffusion d'un laser sur la surface) avec un temps équivalent mais les corrections et la mise en forme peuvent se faire sur une face choisie arbitrairement.

Lors de mes premiers contrôles la lame était à lambda sur deux environ et sur corrigée (j'avais mesuré de façon approximative le diamètre du sphéromètre qui était plus faible que prévu d'où une flèche trop forte) . J'ai fait plusieurs heures de polissage en relâchant légèrement la pression. la lame c'est améliorée de façon cohérente jusqu'a environ lambda sur 5 cf figure ci dessous.

Amélioration de la forme de la lame en cours de polissage en recalant légèrement la pression; entre chaque courbe il y a environ 1 heure de polissage l'axe y est gradué en mµ

Si on est scrupuleux dans les mesures je pense que l'on peut pratiquement obtenir d'emblé une lame avec une précision de lambda/4.

Pour aller plus loin, j'ai réalisé des retouches par surpression comme pour paraboliser un miroir. La précision obtenue est au Foucault proche de lambda/16 ce qui assure à coup sur une très bonne lame. La précision peut être importante car la surface est très douce compte tenu de la méthode et l'erreur sur la surface peut être quatre fois plus importante que sur un miroir.

Forme finale de la lame réalisée: en haut surface d'onde en bas les écarts lambaF/ro

à gauche Ronchigramme du miroir sphérique, à droite Ronchigramme de la lame qui montre la régularité de la forme.

Une seule structure assemble le primaire, le secondaire et le système support de la camera au moyen de tubes en carbone pour assurer une faible variation du foyer en température

Le barillet du primaire (épaisseur 25mm) est constitué de 3 triangles, les butées latérales sont des roulements à billes.

Le support du secondaire permet le réglage de la distance primaire secondaire (critique) . Le secondaire est porté sur un support pouvant être orienté

Le support de la camera est constitué par une platine permettant de faire la mise au point au moyen d'un moteur pas à pas. La camera viens se fixer au milieu du faisceau

L'ensemble de la structure est logée dans un tube en contreplaqué. A l'extrémité du tube se trouve le barillet support de la lame correctrice.

Après un réglage rapide par temps de pluie camera ASI1600 l'arrivée du téléphérique de Chamrousse à 24km

© Jean DIJON : Tous les documents présents sur ce site sont protégés par les lois sur les droits d'auteur.
La reproduction et la diffusion de ces documents sont interdites sans le consentement de l'auteur.

distance miroir lame	152.8	cm
distance secondaire	48.4	cm
distance secondaire foyer	33.8	cm

focale	1056.2	mm

longueur tube	159	cm