1 Super polissage et contraste de phase
1.1 théorie du contraste de phase
1.2 réalisation de la lame de phase
Introduction
1) Super polissage et contraste de phase
Le super polissage ou polissage avec une rugosité très faible nécessite pour être réalisé un moyen de contrôle. Cette technique accessible à l'amateur est le contraste de phase inventé par F. Zernike et redécouverte par B. Lyot qui l'a appliqué à l'étude de la rugosité des surfaces polies [27].
1.1 théorie du contraste de phase
Les lignes qui suivent sont inspirées du Bruat [26] p323 et de M. Françon [28]
La méthode du contraste de phase permet l'étude des objets transparents "ne présentant que des variations locales d'indice ou d'épaisseur"
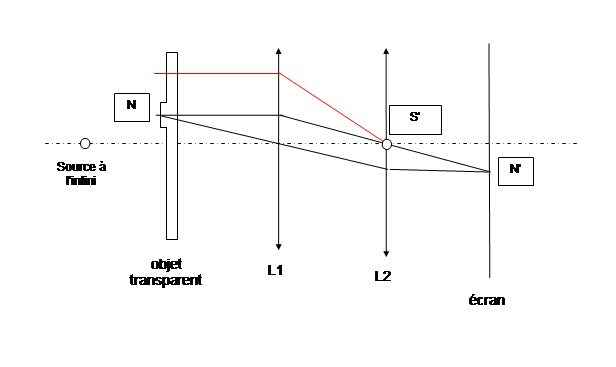
Le dispositif optique de base est présenté ci dessous:

Un objet transparent O (qui ensuite sera la face de la lentille ou du miroir à étudier) est éclairé en faisceau parallèle par une source S placée à l'infini. Cet objet comporte une petite zone N d'épaisseur différente. Cette zone crée une onde par diffraction . Une lentille L1 proche de O image la source à son foyer S' ou une deuxième lentille L2 image la zone N en N' sur un écran. Au point N(x,y) l'amplitude lumineuse et la phase peuvent être représentées par une fonction complexe
f(x,y)=A(x,y) exp(i φ(x,y))
A représente l'amplitude lumineuse et phi la phase. On admet que A est constant sur l'objet (objet parfaitement transparent ). La phase phi est reliée à la variation du chemin optique δ induite par les variations d'épaisseur Δe (ou d'indice) de l'objet. Pour un objet dans l'air d'indice n présentant des variations d'épaisseur on a
φ(x,y)= 2π(n-1)Δe(x,y)/λ=2πδ/λ
si φ est petit (rugosité) on a f(x,y) =A (cos(φ) + i sin(φ)) ≈A(1+i φ) =A(1+e(iπ/2)φ)
On voit que l'onde lumineuse dans le plan image est la somme de l'onde principale non affectée par les irrégularités de l'objet (A*1) plus d'une onde secondaire en quadrature (i=déphasage de pi/2) dont l'amplitude A φ(x,y) varie localement. L'onde secondaire est due à la diffraction des ondes lumineuses par les irrégularités de l'objet . L'onde principale couvre toute la surface de la lentille L1 donc au foyer S' cette onde donne lieu à une tache de diffraction très fine ayant un diamètre angulaire de l'ordre de 2*1.22*lambda/D D étant le diamètre de lentille. Les ondelettes créées par une bosse de diamètre b donne lieu à une tache de diffraction beaucoup plus étendues de diamètre 2*1.22*lambda/b d'autant plus étendue que b (largeur du défaut ) est petit . On a donc dans le plan focal une séparation des deux ondes ce qui permet de modifier les vibrations de l'une sans modifier les vibrations de l'autre. C'est le principe de la strioscopie et du contraste de phase.
La strioscopie consiste à introduire sur le trajet lumineux en S' un petit écran opaque qui bloque l'onde principale (en rouge sur la figure ci dessus). La taille de l'écran est telle qu'il couvre la tache centrale et les premiers anneaux de diffraction de l'image de S en S'.
Dans ces conditions l'éclairement dans le plan image est proportionnel à (A φ)2 , les images des bosses et des creux de l'objet apparaissent en clair sur fond noir. Il faut un éclairement très intense et dans ces conditions l'écran obturateur laisse passer une partie plus ou moins importante du flux incident . Il en résulte un voile sur l'image qui détermine le contraste donc la visibilités des défauts.
Par exemple [26] si δ=(n-1)Δe/λ=8nm λ=550nm on φ=1/10rd l'éclairement est alors de 1/100 de celui de l'onde directe.
Le contraste de phase consiste à remplacer l'écran opaque en S' par une lame qui déphase l'onde principale d'un angle que l'on prends en général égal à π/2, l'épaisseur optique de la lame est dans ce cas de λ/4 (2πδ/λ=π/2)
Dans ces conditions l'onde principale et secondaire peuvent interférer et l'éclairement I1 de l'image est A2(1+φ)2≈A2(1+2φ)
On voit que l'éclairement est maintenant proportionnel à φ donc si phi est positif (cavité avance de phase) l'éclairement est plus important et si phi est négatif (bosse retard de phase ) l'éclairement est moins important que le fond de l'image. Le contraste de visibilité γ des détails est défini par
γ=(I1-I0)/I1 ou I0 est l'éclairement du fond (A2) donc
γ=2φ/(1+2φ)≈2φ
La sensibilité peut être fortement améliorée en absorbant partiellement l'onde principale. Si on divise l'intensité de la lumière par N (lame de phase avec une densité optique D=log10(N))
on a I1 = A2(1/N1/2 +φ)2 ≈ (A2/N)(1+2φN1/2) (1)
d'ou le contraste γ=2φN1/2 (2)
Si on divise l'intensité de l'onde primaire par 100 on augmente le contraste par 10 pour une lame de phase produisant un déphasage de π/2
Si le déphasage de la lame n'est pas exactement π/2 :
υ est le déphasage, on a alors f =A(1+ei(π/2-υ)φ) et l'intensité dans l'image est A2(1+ 2φsin(υ)) pour une lame absorbante on a donc un contraste
γ=2φsin(υ)N1/2 (3)
Si la source S n'est pas monochromatique :
l'image est la somme des images monochromatiques. Si la différence de marche ne varie pas trop avec la longueur d'onde on observe toujours le phénomène.
Si le déphasage est réalisé avec du verre et que l'épaisseur et l'indice sont telles que l'on ai un déphasage de π/2 pour la raie F (0.486µm) on a
υf=2π(nf-1)/λf=π/2 le déphasage de la lame pour la radiation C (0.646µm) rouge est υc=2π(nc-1)/λf=π/2*(λf/λc)*(nc-1)/(nf-1)
pour du BK7 nf= 1.5224 nc=1.5143 d'ou vf=1.16 le contraste dans le rouge est donc 2φsin(vf)=1.84φ au lieu de 2φ
le contraste ne change donc pratiquement pas (pour une lame transparente) en fonction de la longueur d'onde
1.2 réalisation de la lame de phase
La lame de phase doit permettre le contrôle de la phase et de la densité de l'onde primaire sur une bande étroite, la source étant généralement une fente. Le reste de la lame est transparente pour laisser passer le flux diffracté.
On peut obtenir un dépôt métallique semi transparent par dépôt sous vide. On donne au dépôt la forme voulue (trait) et on obtient une différence de phase de pi()/2 entre les rayons qui traversent la couche métallique et les rayons qui traversent le support lorsque la densité de la couche est suffisante. figure a) ci dessous
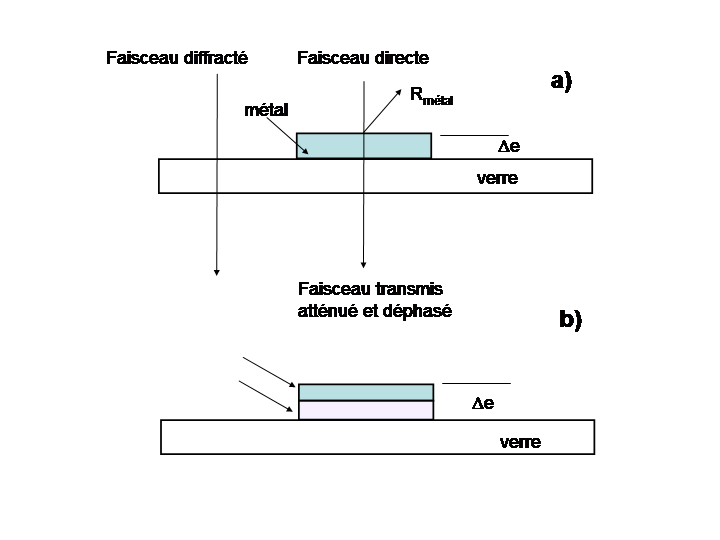
Une variante figure b) consiste à empiler une couche absorbante et une couche transparente. La couche transparente contrôle le déphasage, la couche absorbante la densité de la lame.
B. Lyot a réalisé un compensateur de ce type en utilisant une lame de verre à faces non parallèle formant un coin de très petit angle (1minute) sur lequel il a déposé un absorbeur (aluminium plus noir de fumé)
la partie absorbante a été coupée et peut se déplacer par rapport au reste de la lame figure ci dessous. Le déplacement de la partie absorbante permet de régler précisément la phase
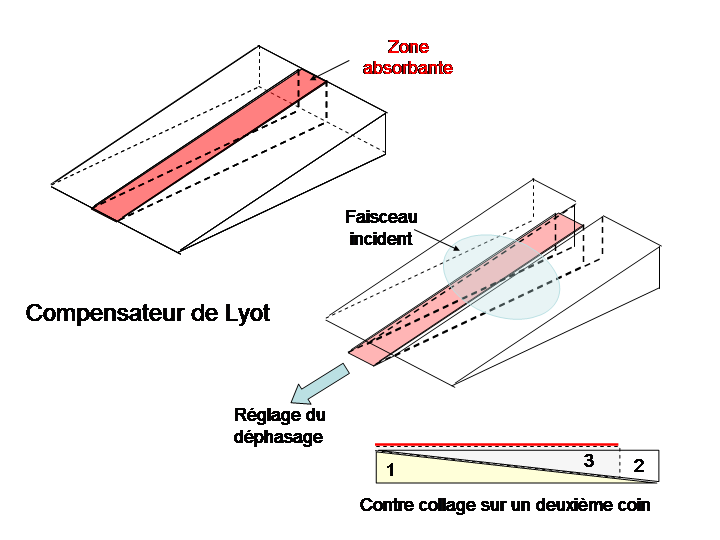
évidemment un tel composant est difficile à réaliser par des amateurs. le déplacement longitudinale d'un mm de la languette fourni un déphasage de pi/2 environ.
Les premiers essais fait par Lyot ont été réalisés avec un coin juste coupé en deux une des moitié étant recouverte de noir de fumé et d'une fine couche d'aluminium sur une certaine largeur le reste de la moitié étant masqué par un écran opaque, les deux moitiés glissent l'une par rapport à l'autre. Seulement 50% du flux diffracté était recueillit du coté transparent de la lame . Dans le compensateur décrit ci dessus la languette mobile fait 0.7mm de large.
Les lames mince métalliques ont été étudiées par F. Abéles et décrites par Françon [28]. Pour l'aluminium les courbes suivantes traduisent le déphasage en fonction de la densité pour λ=0.546µm
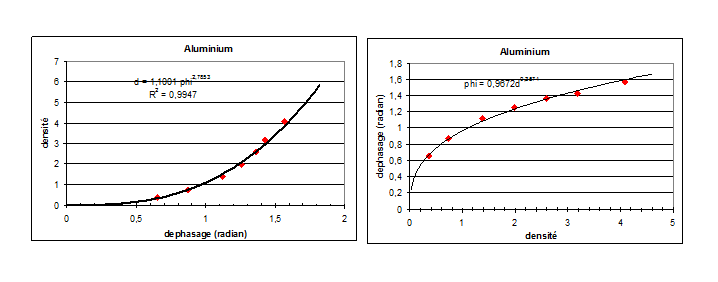
On a: φ=0.9672D0.3571
on voit que pour l'aluminium il faut des lames relativement absorbantes (10-3 à 10-4 de transmission ) pour obtenir un déphasage proche de pi/2.
Si on considère une lame mince métallique d'épaisseur l suffisamment absorbante pour qu'il n'y ait pas de multi réflexion à l'intérieur du métal la transmission T de la lame vaut :
T= ((n+1)2-(n-1)2)/((n+1)2+k2)exp(-αl) ou l'indice du métal est n, k est son coefficient d'extinction et α=4πk/λ est le coefficient d'absorption.
on a le tableau suivant en fonction de l'épaisseur l de la couche d'aluminium pour lambda=0.546µm (n=0.77 k=5.8)
| l (µm) | 0,0050 | 0,0100 | 0,0150 | 0,0200 | 0,0250 | 0,0300 | 0,0350 | 0,0400 | 0,0450 | 0,0500 | 0,0550 | 0,0600 |
| T | 0,04322 | 0,02215 | 0,01135 | 0,00582 | 0,00298 | 0,00153 | 0,00078 | 0,00040 | 0,00021 | 0,00011 | 0,00005 | 0,00003 |
| D | 1,36 | 1,65 | 1,94 | 2,24 | 2,53 | 2,82 | 3,11 | 3,40 | 3,69 | 3,98 | 4,27 | 4,56 |
il faut environ 50nm d'épaisseur pour avoir un déphasage de pi/2 ce qui donne des lames très absorbantes
pour lambda= 0.4358µm (longueur d'onde utilisée par Texereau [29]) n=0.45466 k=4.66 on a:
| l (µm) | 0,0050 | 0,0100 | 0,0150 | 0,0200 | 0,0250 | 0,0300 | 0,0350 | 0,0400 | 0,0450 | 0,0500 | 0,0550 | 0,0600 |
| T | 0,03977 | 0,02042 | 0,01049 | 0,00539 | 0,00277 | 0,00142 | 0,00073 | 0,00037 | 0,00019 | 0,00010 | 0,00005 | 0,00003 |
| D | 1,40 | 1,69 | 1,98 | 2,27 | 2,56 | 2,85 | 3,14 | 3,43 | 3,72 | 4,01 | 4,29 | 4,58 |
on peut en conclure que les lames utilisées par Texereau avait des épaisseur d'environ 10nm (D=1.69) et 30nm (D=2.81) les déphasages étant de 1.1 et 1.4 rd proche de pi/2 pour les lames les plus absorbantes.
pour lambda=0.6563µm dans le rouge n=1.2829 k=6.91 on a:
| l (µm) | 0,0050 | 0,0100 | 0,0150 | 0,0200 | 0,0250 | 0,0300 | 0,0350 | 0,0400 | 0,0450 | 0,0500 | 0,0550 | 0,0600 |
| T | 0,04989 | 0,02562 | 0,01316 | 0,00676 | 0,00347 | 0,00178 | 0,00091 | 0,00047 | 0,00024 | 0,00012 | 0,00006 | 0,00003 |
| D | 1,30 | 1,59 | 1,88 | 2,17 | 2,46 | 2,75 | 3,04 | 3,33 | 3,62 | 3,91 | 4,20 | 4,49 |
On voit que pour l'aluminium la densité change peu avec la longueur d'onde, pour la phase c'est moins claire faute de données. En particulier avec l'aluminium n est inférieur à 1 jusqu'a 600nm et devient supérieur à 1 dans le rouge le signe de la phase change donc autour de 600nm. Il vaut donc mieux utiliser ces lames vers les courtes longueurs d'onde (bleu ou vert)
F. Abelés donne pour l'aluminium à λ=0.546µm un déphasage qui s'écrit en fonction de l'épaisseur φ=φ0+2πl/λ(ns-nal). La figure ci dessous représente les données mesurées
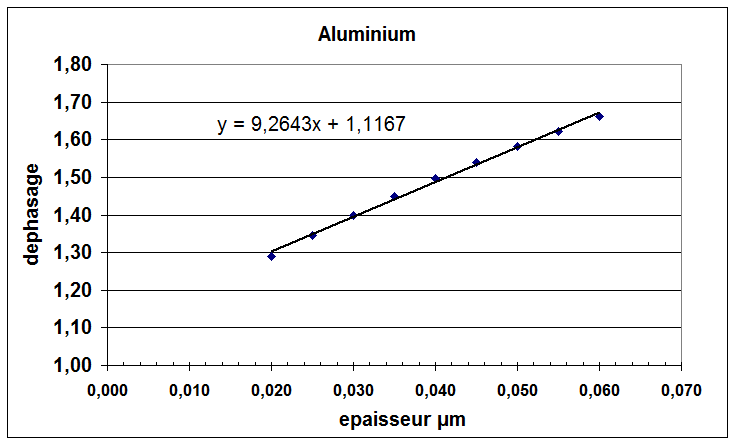
On trouve en ajustant les données expérimentales avec cette formule un indice de la couche d'aluminium de 0.72 alors que les tables (de l'aluminium massif) donnent 0.77
ce qui n'est pas si mal ni étonnant pour des couches minces obtenues par évaporation donc moins dense que de l'aluminium massif.
En conclusion si on veut réaliser une lame de phase avec une couche d'aluminium pas trop dense sur du verre on prendra plutôt:
_pour D=2.5 une épaisseur de l'ordre de 25nm qui fourni une phase de +pi/2.34 et un contraste de 1.95 φ 17.78 = 34 φ
un défaut de 1 Angstrom sur l'onde apparaîtra avec un contraste de 34*2pi*x/λ = 4% à 0.546µm
Les couches d'aluminium se couvrent très rapidement d'une couche d'alumine dont l'épaisseur est de l'ordre de 4nm [ ] ,alumine qui épaissi avec le temps donc la densité de la lame vas avoir tendance à diminuer sur plusieurs années.
_avec de l'argent on peut obtenir des couche moins dense D=2 pour un déphasage de pi/2, F. Abéles donne une épaisseur de 50nm pour un déphasage de +pi/2
un défaut de 1 Angstrom sur l'onde apparaîtra dans ce cas avec un contraste de 20*2pi*x/λ = 2.3%
La figure ci dessous donne une idée de la variation de la phase et de la densité de couches d'argents en fonction de l'épaisseur en tenant compte des données de la littérature
Pour une densité de 2 le calcul fourni une épaisseur un peu plus fine que ce que donne Abéles mais ce ne sont que des calculs indicatifs et les indices des couches sont différents des indices des matériaux massifs.
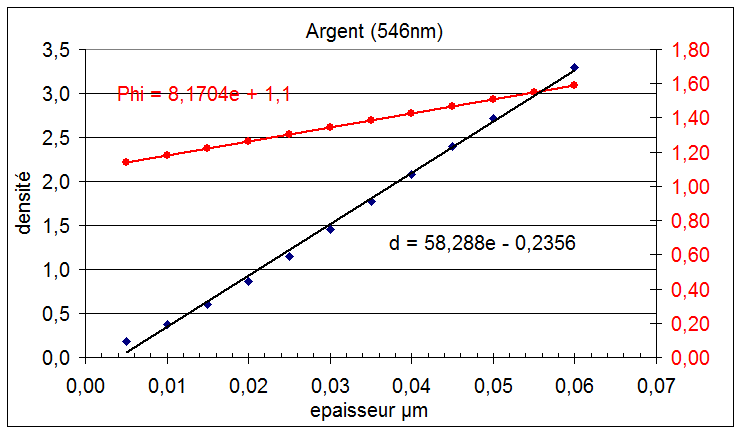
Au niveau amateur on peut envisager de faire de telles lame en réalisant une argenture chimique partielle en utilisant par exemple la recette de Texereau [3] .
Dans tout les cas il faut faire des essais .
Le moyen le plus simple pour l'amateur est d'utiliser du noir de fumé! Il semble que de telles lames fonctionnent [30]. Leur réalisation est la suivante:
_on part par exemple d'une lame de microscope comme support, ou de tout autre support en verre. Le mieux est que la taille du support couvre l'objectif photo qui sera utilisé par la suite
_on passe lentement et régulièrement la lame au dessus d'une bougie allumée pour que le noir de fumé se dépose sur le verre. La lame doit être proche de la flamme. La lame peut être tenue par un statif pour contrôler sa hauteur par rapport à la flamme
_On peint littéralement la lame pour obtenir un dépôt uniforme. Si le dépôt n'est pas uniforme on nettoie la lame avec un chiffon et on recommence. C'est un des intérêts de la méthode 10 à 15 passages au dessus de la bougie sont normalement suffisant .
_La densité à atteindre est typiquement de 2 (1% de transmission) on peut comparer la densité de la lame avec celle d'un filtre neutre photographique ND128 par exemple. La densité est telle que l'on peut lire les caractéristiques d'une ampoule de 60W éclairée sans aucun éblouissement.
Il faut ensuite créer une bande étroite (1mm à 2mm de large) absorbante au milieu de la lame de verre en enlevant (grattant) l'excès de fumé au moyen d'une carte de visite par exemple que l'on guide avec un réglet pour avoir un bord net. On peut également réaliser une fente avec un masque et faire le dépôt à travers le masque.
La couche réalisée est incroyablement fragile. Pour fixer le trait on peut utiliser de l'alcool. On immerge extrêmement lentement la lame dans de l'alcool iso pour ne pas laisser de traces(qq mm au fond d'un récipient à fond plat et on attend que cela sèche!). Le dépôt de carbone est ainsi moins fragile.
Bigowlbinoscope peut fournir des lames de phase en chrome de densité 2.5 à 650nm https://bigowlbinoscope.fr/ déposées sur des lames de microscope.
L'indice du chrome est élevé, supérieur à 1 contrairement à l'argent et l'aluminium, le déphasage est négatif dans ce cas donc les reliefs sont inversés par rapport à l'aluminium ou l'argent mais cela n'a pas beaucoup d'importance (une cavité apparaît brillante).
On peut comme précédemment simuler le comportement optique de cette lame.
Pour le chrome on a les indices suivants (matériau massif):
| lambda (nm) | n | k | alpha (nm-1) |
| 660 | 3,0891 | 3,3411 | 0,063614395 |
| 600 | 3,1943 | 3,3 | 0,069115038 |
| 546 | 3,1543 | 3,33 | 0,076641052 |
| 500 | 2,7804 | 3,3048 | 0,083058683 |
| 450 | 2,323 | 3,135 | 0,087545715 |
| 400 | 2,015 | 2,8488 | 0,089497692 |
Ce qui permet de calculer la phase et la densité de la lame. Avec ces données l'épaisseur théorique du chrome est de 79nm pour avoir un déphasage de pi/2
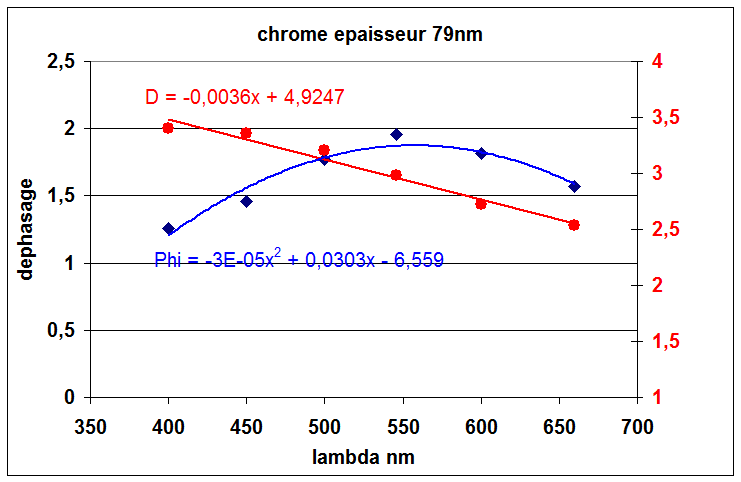
Pour une telle lame on peut établir le tableau suivant qui fourni en dernière colonne le contraste d'un défaut de 0,1nm (1 angstroem) sur l'onde pour différentes longueur d'ondes
| Lambda | 2sin(v)racine(D) | contraste γ |
| 660 | 37,1 | 0,03531912 |
| 600 | 44,4 | 0,04649557 |
| 546 | 57,3 | 0,06593892 |
| 500 | 78,5 | 0,09864601 |
| 450 | 94,6 | 0,13208652 |
| 400 | 95,4 | 0,14985397 |
On voit que la lame est à priori 4 fois plus sensible dans le bleu que dans le rouge. Cela provient (contrairement aux lames transparentes et à l'aluminium) de l'augmentation importante de la densité.
La figure ci dessous décrit le dispositif pour contrôler un miroir parabolique. A droite le dispositif décrit par Texereau
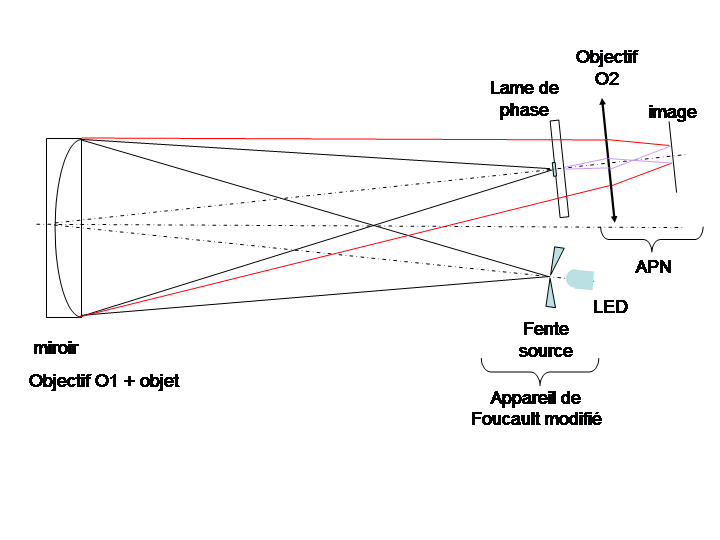
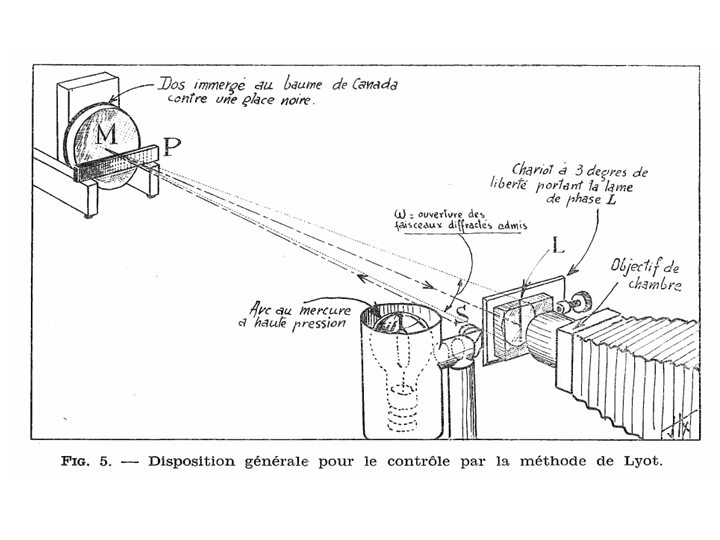
On peut utiliser un dispositif de Foucault comme source d'illumination avec une fente assez large 20 à 100µm et une led puissante comme source. La lame remplace le couteau et ses mouvements lents servent au réglage de la lame. Comme le miroir présente une aberration sphérique en son centre de courbure (miroir parabolique) on place la lame au niveau du cercle de moindre aberration (zone 0.7). Le trait doit recouvrir l'image de la fente ainsi que la lumière diffractée autour de l'image de la fente. On utilise un appareil photo numérique derrière la lame mis au point sur le miroir pour récupérer l'image. J'utilise un télé de 200mm qui couvre bien mon capteur 24*36 . La lumière étant très faible il convient d'opérer dans le noir en limitant toute les lumières parasites. Le dos du miroir est une source de lumière parasite si on test un miroir en cours de polissage. Il convient de doucir le dos sachant que la partie centrale du miroir peut renvoyer de la lumière diffuse dans le cône de mesure. Les temps de pose peuvent faire plusieurs dizaines de secondes.
On s'applique à centrer l'image de la fente sur la bande absorbante pour avoir une image symétrique.
Quantification du test de Lyot:
Les premières mesures de Lyot correspondant à sa publication [27] sont reproduites ci dessous:


on voit que la lame de phase a la structure suivante (figure ci dessous) et était utilisée avec un cache sur pratiquement la moitié de sa surface:
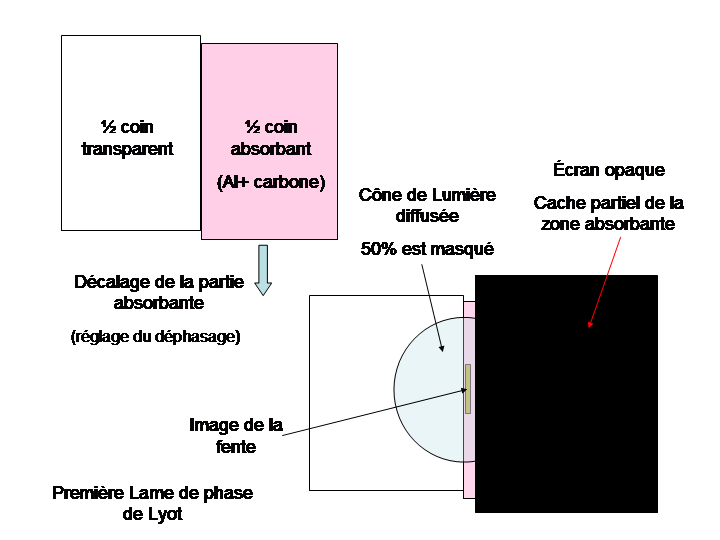
En particulier uniquement 50% du flux diffracté par la surface du miroir est recueilli, il en résulte le facteur K=0.5 utilisé ci dessous dans la formule (4).
A la fin de l'article Lyot décrit le compensateur représenté figure 3 pour lequel K=1 (K est la proportion des radiations diffractées qui atteignent l'objectif)

Dans son article Lyot présente l'utilisation d'un coin photométrique pour mesurer le contraste des défauts.
L'intérêt est, à l'époque des plaques photo argentiques (non linéaires), d'intégrer une échelle photométrique dans l'image et surtout de ne pas avoir à connaître précisément la densité de la lame . Le coin photométrique est composé d'un coin transparent et d'un coin absorbant. Il permet d'avoir une relation linéaire entre l'absorption et la position sur le coin.
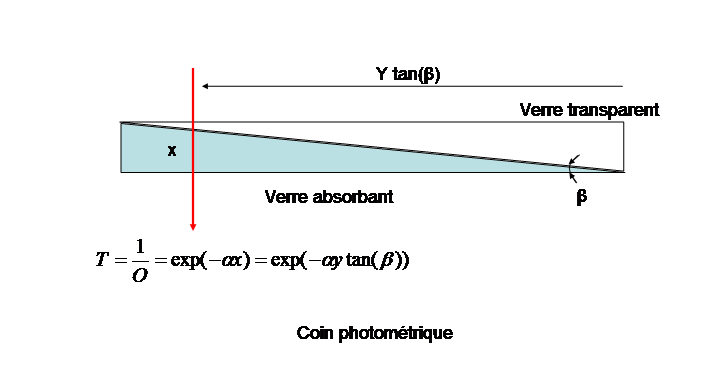
B. Lyot donne la formule suivante en fonction des opacités des points du coin correspondant aux densités du fond et des détails

Pour comprendre cette expression on part de la formule (1) . Comme D =log10(O) on a I0/O'=I0/O(1+2πx/λ(KO)1/2)2 KO est le flux provenant des défauts compte tenu de la perte lié au cache..
En prenant la racine carrée des 2 membres:
√(O/O')=(1+2πx/λ√O√K) ou x est la hauteur du défaut sur l'onde
d'où la formule de Lyot en divisant par √O xonde=λ/(2π√K)(1/√O'-1/√O) (4)
Si on utilise juste un trait déphasant et non un cache sur 50% de la lame on a K≈1
Dans le montage de Texereau la lumière passe deux fois dans le coin à cause de la réflexion sur le miroir donc la densité du coin doit être multiplié par 2
Sur le verre dans le cas d'un miroir, le défaut Δe est deux fois plus petit car on a xonde=2Δe à cause de la réflexion.
Si on a pas de coin absorbant (cas des amateurs) on peut mesurer le contraste des défauts en utilisant une image d'APN qui normalement est linéaire
Il faut par contre connaître le déphasage et la densité de la lame pour donner une valeur chiffrée en nm de la rugosité.
on a: γ=2φsin(υ)N1/2 =4πxonde/λ√N d'où
xonde=γλ/(4πsin(υ)√N)=(Ifond/Idefaut-1) λ /(4πsin(υ)√10D) (5)
Exemple: pour λ=650nm avec une lame en chrome de densité D=2.5 √102.5= √316=17.8 si Ifond=128 Idéfaut=110 on a avec la formule (5)
xonde=(128/110-1)*650/4/3.14/17.8=0.48nm soit environ 2.4Ǻ sur le verre
Exemple de surface de miroirs :
T210mm nu
J'ai utilisé ce miroir pour faire des essais de super polissage. La partie centrale est plus diffusante à cause du dos.
La coupe d'une partie de l'image (couche rouge) est présentée ci dessous:
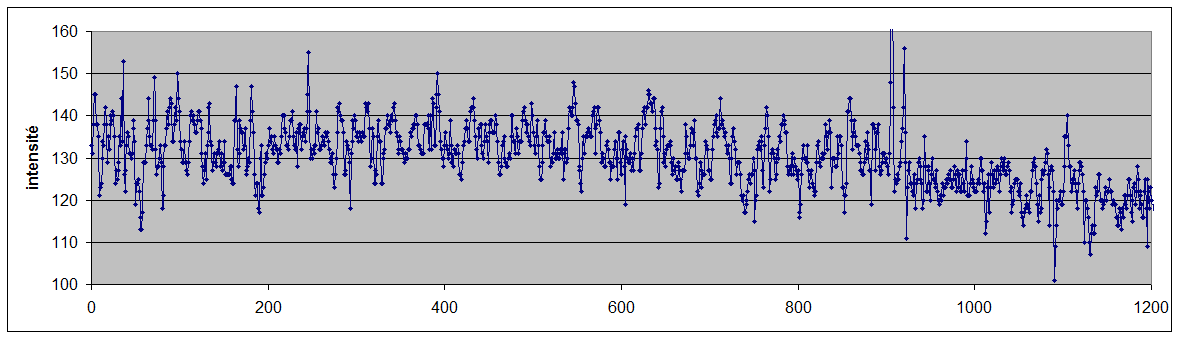
l'histogramme cumulé ci dessous suit très bien une loi normale on peut donc calculer la moyenne et l'écart type de la distribution pour évaluer la rugosité RMS.
On a Ifond= moyenne = 129.8 et Idefaut =moyenne - écart type= 121.9 ce qui donne un contraste de défaut de 0.065
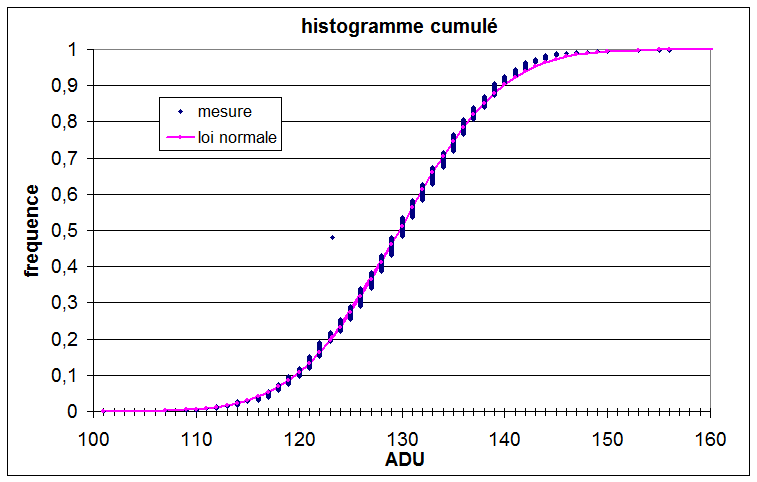
on en déduit compte tenu de la densité de la lame (2.5) et de l'équation (5) une rugosité RMS de 0.19 nm si on exploite les 3 couches couleurs on obtient le résultat suivant:
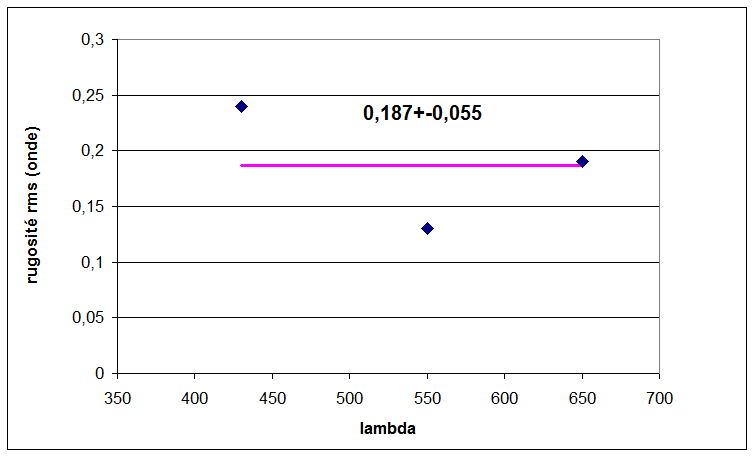
résultats cohérents en fonction de la longueur d'onde, les écarts étant certainement liés aux indices réels de la couche forcement différents des indices du chrome massif . La rugosité du miroir est donc autour de 2A RMS ce qui n'est pas encore du super poli mais très doux. On peut espérer gagner un facteur de 4 ou 5 sur la diffusion en améliorant le polissage.
T310mm aluminisé
Le miroir ci dessus présente de nombreuses piqûres et poussières (points blancs) sur l'aluminure qu'il est impossible de nettoyer. Des coupes photométriques sur le bas du miroir fournissent avec la même lame que le miroir de 210mm une rugosité de 2.3A RMS ce qui confirme que l'aluminium ne change pas la rugosité (aux fréquences spatiales qui nous intéressent) et que la rugosité dépends essentiellement de l'opérateur et de sa technique de polissage (les deux miroirs étant réalisés par mes soins).
T210 mm super poli par bigowlbinoscope image aimablement communiquée pat T. Pelletier
Miroir super poli réalisé par Térence Pelletier de bigowlbinoscope. Ce miroir est plus doux que le 210mm présenté plus haut il est donné à 1A rms par T. Pelletier. La lame de phase utilisée est sans doute un peu différente de la mienne car elle absorbe beaucoup plus le bleu (d'ou la couleur jaune).

T305mm super poli en quartz
Ce miroir déformé par dépression a donc été super poli sphérique, la rugosité est très bonne de l'ordre de 0.5A rms à comparer au T200mm décrit au dessus. Une partie du gain provient de la plus grande dureté du quartz mais également de la technique de polissage. La comparaison est significative car les résultats sont obtenus avec le même appareillage.

rugosité du miroir obtenu sur une ligne de coupe de l'image
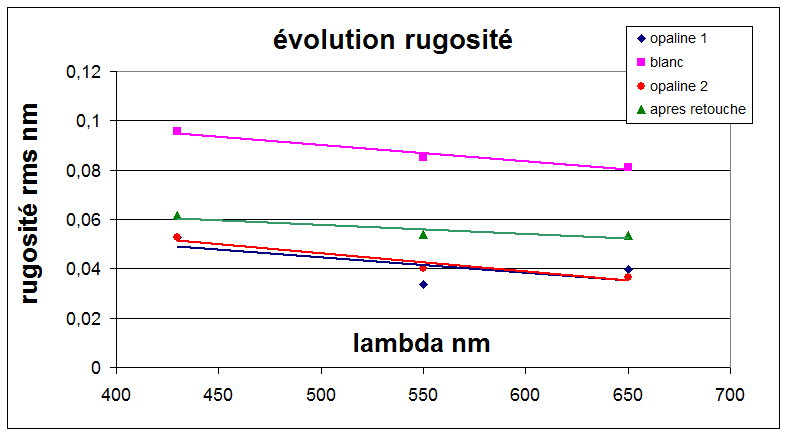
Des essais on été fait en cours de polissage pour évaluer la rugosité en fonction du produit de polissage utilisé. L'opaline permet de gagner un facteur 2 par rapport au blanc ce qui confirme bien l'intérêt de ce produit dont la taille des grains est de l'ordre de 0.3µm.
Le super polissage est un polissage de finition qui fourni de faibles rugosités de surface, typiquement de l'ordre de l'angstroem RMS sur l'onde. La diffusion intégrée TIS (total integrated scattering en anglais) variant comme le carré de la rugosité RMS, si on gagne un facteur 3 sur la rugosité on gagne un facteur 9 sur la diffusion. Remarquons déjà qu'une surface en transmission (lentille) diffuse beaucoup moins qu'un miroir en effet on a:
TIS(reflexion)= (4πσ/λ)2
TIS(transmission)=(2πσ/λ(n-1))2
les deux formules sont identiques avec n=-1 pour la réflexion. Pour n=1.5 on a:
TIS(transmission)=TIS(reflexion)(n-1)2/4=TIS(reflexion)/16 ceci explique pourquoi les coronographes sont des lunettes!
Le traitement du miroir joue un rôle important dans la lumière diffusée [35] [ici]
"While the scattering will scale like RMS roughness squared for values of 1nm or larger, the intrinsic scattering of aluminum coatings will dominate for super-smooth surfaces. Down to 1nm finishes, the quality of the coating required for solar work is ‘standard’. To push levels of scattering below 10ppm, great care will have to be given to the coating. Even with perfect coatings, the refractor has a factor of 10 lower scattered light than a reflector with the same polish quality".
Alors que la diffusion évoluera comme la rugosité RMS au carré pour des valeurs de 1 nm ou plus, la diffusion intrinsèque des revêtements d'aluminium sera dominante pour des surfaces ultra-lisses. Jusqu'aux finitions de 1 nm, la qualité du revêtement requis pour le travail solaire est « standard ». Pour pousser les niveaux de diffusion en dessous de 10 ppm,il faudra faire très attention au revêtement. Même avec des revêtements parfaits, le réfracteur a un facteur de lumière diffusée 10 fois inférieur à celui d'un réflecteur ayant la même qualité de polissage.
On peut donc se poser des questions sur l'intérêt réel d'un miroir super poli ( dans le cas d'un miroir aluminé ).
Quel est l'intérêt de diminuer la diffusion et dans quel type d'observations est ce important? Typiquement, ce point est capital pour l'observation d'objets faibles proche d'une source intense. Le meilleur exemple étant la couronne solaire qui est environs 1million de fois plus faible (moins lumineuse) que le soleil. D'autres observations comme phobos et deimos ou Sirius B nécessitent une diffusion très faible. Après il est souvent dit que l'observation planétaire ou l'on veut observer de très faibles contrastes gagne à l'utilisation d'un miroir super poli.
Quelles sont les conditions d'obtention d'une faible rugosité? La valeur moyenne de la rugosité Ra s'exprime par [34]
Ra =CEp2/3P1/3d/Hw (6)
ou Ep est le module d'Young du polissoir P est la pression appliquée d est la taille des particules de polissage et Hw est la dureté de la pièce optique
On voit donc qu'il faut polir une pièce dure avec de petites particules et un polissoir mou.
Voyons ce qu'en dit André Couder [29]:

Le point clef dans cette description est " le poli le plus pur apparaît au moment ou le rouge étant complètement écrasé et chassé l'outil menace d'adhérer au verre"
Le problème souligné est de réaliser simultanément la forme optique et la faible rugosité.
On trouve au niveau amateur un ensemble de recommandations pour réaliser une surface super poli. Ces recommandation données en vrac sont:
- 1) utilisation de mouvements très doux (non saccadés)
- 2) utilisation de produits à polir genre opaline (oxyde de cérium qui a des grains de l'ordre de 0.3µm)
- 3) utilisation de poix mole avec des carrés très fin
- 4) polissage à l'eau
- 5) utilisation d'un produit de polissage secret ?
Les points 2 et 3 (voir 5) sont en accord avec l'équation (6)
J'ai fait des essais avec de la poix standard et des mouvements très doux avec du rouge à polir, de l'opaline et de l'oxyde de zirconium (blanc).
Les résultats sur un miroir de 210mm sont ici , la rugosité dans tout les cas est autour de 2 Angstroem.
Donc des mouvement très doux ne suffisent pas à obtenir un super poli (rugosité de l'ordre de l'angstroem) quelque soit le produit à polir.
J'ai ensuite réalisé un miroir en quartz en utilisant lors de la finition un produit à polir industriel vendu par Aqualam: l'Aqualine M.
Ce produit à deux effets:
_ Sur une poix de dureté normale il a tendance à faire fondre (fluer) la couche superficielle de la poix lui procurant une faible rugosité. Par ailleurs la poix devient collante en surface
_ En utilisation, l'adhérence du polissoir devient extrême et on arrive à sécher pratiquement complètement la surface. Une fois l'Aqualine utilisée cette caractéristique du polissoir subsiste un certain temps même si on poli classiquement avec de l'opaline ou du blanc.
On réalise ainsi grâce à ce produit, un polissoir qui reste assez ferme mais dont les carrés de poix ont une couche superficielle très mole. Cette caractéristique est à rapprocher de l'utilisation de carrés de poix très fins et très mous.
Je pense que grâce à ce produit on se trouve, même avec une poix non extra mole, dans les conditions décrites par A. Couder (l'outil menace d'adhérer au verre).
Il faut donc qu'il y ait une adhésion considérable du polissoir sur le verre avec une quantité de produit abrasif très faible pour niveler la surface à une échelle de l'ordre de l'angstroem.
Reste le problème de la mise en forme, il faut voir que cette étape de finition est réalisée à la fin avec un miroir qui peut être considéré comme pratiquement terminé. Il faut donc trouver une méthode pour polir dans ces conditions particulières sans dégrader la forme obtenue. Pour l'instant je n'ai pas fait de miroir parabolique super poli.
Dans le cas du miroir en quartz de 305mm comme la forme asphérique est obtenue par dépression sous vide le polissage est celui d'une sphère donc le problème de la mise en forme asphérique ne se pose pas. La rugosité obtenue est excellente inférieure à 1Angstroem RMS
J'ai fait à cette occasion des mesures de rugosité en fonction du produit à polir utilisé (même opérateur, même polissoir). Il est clair que l'opaline fourni un état de surface deux fois meilleur que le ZrO2 par contre l'opaline est difficile d'emplois. Pour ma part je mélange le ZrO2 avec l'opaline et j'enrichi le mélange à polir en opaline au cours de la séance. Il faut également pressé l'outil à froid longuement avant de commencer.
2) Foucault automatique (sans masque)
Le test de Foucault très décrié (par les gens qui ne taillent pas de miroirs) présente deux faiblesses
_impossibilité de mesurer l'astigmatisme, il faut pour cela utiliser un autre test
_il est dépendant de l'opérateur qui s'il n'est pas intègre, sur évalue toujours la qualité de son miroir.
Pour remédier à ce dernier point il existe aujourd'hui des tests impersonnels en particulier un test sans masque que l'on peut trouver sur cloudy night
que je trouve très pratique. Il est gratuit. Il faut un appareil photo et faire des images de la surface vu à travers le Foucault. On fait une série d'images en décalant l'offset du couteau d'une valeur constante entre chaque image par exemple de 0.5mm. Une fois la série de photos réalisée le soft détermine pour chaque image la zone du miroir qui s'éteint
Sinon il y a le programme virtual Couder screen qui est payant (prix raisonnable) il faut une camera vidéo (webcam ou autre) mais cela fonctionne à merveille. C'est le programme que j'utilise aujourd'hui.
La camera utilisée est une ASI1600 et l'objectif est un téléobjectif de 135mm ou 200mm suivant le rapport F/D du miroir. J'utilise firecapture ou shapcap pour faire les vidéos
Le principe est simple on utilise la camera pour imager en temps réel le miroir derrière le couteau du test de foucault. Le programme crée un masque de couder virtuel que l'on vient positionner sur l'image du miroir. On défini la taille et le nombre de zones au moyen du programme. Ensuite point clef le programme scan et compare la brillance des zones de l'écran on ajuste la brillance avec l'appareil de Foucault. Cette comparaison est impersonnelle et très répétable ce qui en fait tout l'intérêt. Les résultats sont très précis. Les données sont exploitées directement au moyen du programme mais peuvent être transférées dans un autre programme pour analyse. Si l'éclairement du miroir n'est pas parfaitement uniforme on peut faire un flat avec le couteau complètement escamoté avant de faire les mesures. En plus le programme peut déterminer le tirage sur une ligne ce qui est très précis même pour des miroirs très ouverts (j'ai testé jusqu'a F4). La correspondance entre les profils déterminés de cette façon et par interférométrie est très bonne.
L'astigmatisme peut être évalué si les données du Foucault obtenues pour 2 (ou plusieurs) orientations du miroir sont reliées par la zone centrale (si un défaut localisé n'existe pas au centre)
© Jean DIJON : Tous les documents présents
sur ce site sont protégés par les lois sur les droits d'auteur.
La reproduction et la diffusion de ces documents sont interdites sans le consentement de l'auteur.