Une description de la nature des perturbations du front d'onde introduites par l'atmosphère sont fournies par le modèle de Kolmogorov basé en partie sur les études de turbulence du mathématicien russe Andrei Kolmogorov. Ce modèle s'appuie sur diverses mesures expérimentales et est largement utilisé dans les simulations d'imagerie astronomique. Le modèle suppose que les perturbations du front d'onde sont provoquées par des variations de l'indice de réfraction de l'atmosphère. Ces variations d'indice de réfraction conduisent directement aux fluctuations de phase , mais les fluctuations d'amplitude ne sont qu' un effet du second ordre tandis que les fronts d'onde perturbés se propagent depuis la couche atmosphérique perturbatrice jusqu'au télescope. Pour tous les modèles raisonnables de l'atmosphère terrestre aux longueurs d'onde optiques et infrarouges, les performances d'imagerie instantanée sont dominées par les fluctuations de phase . Les fluctuations d'amplitude ont un effet négligeable sur la structure des images vues au foyer d'un grand télescope.
Un domaine mouvementé peut être décrit statistiquement par une fonction de structure :
DN(x)=<(N(r+x)-N(r))2>
où x est la séparation entre les points, N est une fonction (par exemple température, indice de réfraction, etc.) et r est la position. La turbulence de Kolmogorov donne :
Dn(x)=Cn2 x2 /3 (2)
où Cn est la constante de structure de l’indice de réfraction. De là, on peut déduire la fonction de structure de phase à l’ouverture du télescope :
Dφ(x)=6.88 (x/r0)5/3 (3)
où la longueur de cohérence r0(également appelée paramètre de Fried) est donné par:
r0=0.185 λ6/5 cos3/5z [∫(C2ndh]-3/5 (4)
où z est l'angle zénithal, λ est la longueur d'onde. En utilisant la théorie de l’optique, on peut convertir Dφ sous forme d’image. Physiquement, r0 est inversement proportionnel à la taille d de l'image qui vaut :
dturb=0.98 λ/r0 (5)
cette taille est plus importante que la taille de l'image provenant d'images limitées par diffraction :
ddiff=1.22 λ/D (6)
dturb domine quand r0<D, un r0 plus grand signifie avoir une meilleur resolution. La turbulence est plus importante que la diffraction aux longueurs d'onde plus courtes (et pour les ouvertures plus grandes), la diffraction est plus importante aux longueurs d'onde plus longues (et pour les ouvertures plus petites), les effets de diffraction et de turbulence se croisent dans l'IR pour la plupart des télescopes de taille astronomique (autour de 5 microns pour un miroir de 4 m), le croisement tombe à une longueur d'onde plus courte pour un télescope plus petit ou pour un meilleur seeing. Comme on peut s'y attendre, r0 est variable d'un site à l'autre et également dans le temps. Sur la plupart des sites d'observation, il semble y avoir trois zones : la "couche de surface" (interactions vent-surface et vision artificielle), la "couche limite planétaire" (influencée par le réchauffement diurne) et ``l'atmosphère libre'' (avec un fort cisaillement du vent, à 10 km d'altitude c'est la tropopause). Un site astronomique typique a un r0 de quelques cm à 5000A de longueur d'onde. Il faut également considérer la cohérence du même motif de turbulence dans le ciel : l'angle de cohérence appelé angle d'isoplanétique, la région sur laquelle le modèle de turbulence est le même est appelée la zone isoplanétique. L'angle d'isoplanétisme s'exprime par:
θ=0.314 r0/H (7)
où H est la distance moyenne de la couche turbulente :
H=sec z [∫(Cn2h5/3 dh/∫(Cn2dh)]3/5
Sur un site astronomique typique où nous avons r0=10cm pour l'optique, et H=5000m, θ sera en seconde d'arc (arcsec).
θ=0.314*10*10-2/5000 =6 10-6 rd =1.3 arcsec
Dans l'infrarouge où ro sera plus proche du m (ici 70cm)
θ=0.314*70*10-2/5000 =4.4 10-5 rd =9 arcsec
En réalité, les fluctuations de phase dans l’atmosphère ne suivrent la fonction de structure présentée par l’équation (3) que sur une plage finie d’échelles de longueur. L'énergie turbulente est injectée à grande échelle par le cisaillement du vent. La majeure partie du cisaillement du vent devrait se produire dans des couches distinctes de l'atmosphère, et les plus grandes structures turbulentes devraient s'insérer dans l'une de ces couches atmosphériques. L'échelle de longueur à laquelle la fonction structurelle de la turbulence de Kolmogorov se décompose à grande échelle est appelée l'échelle externe de la turbulence ( L0). Plusieurs tentatives ont été faites pour mesurer la taille de cette échelle extérieure en utilisant diverses méthodes différentes, mais les valeurs mesurées varient considérablement. Le modèle de Von Karman (Ishimaru, 1978) devrait décrire la forme du spectre de puissance pour les fluctuations de phase sur des échelles de longueur plus grandes que l'échelle extérieure. Si l'échelle extérieure est plus grande que le diamètre du télescope, alors la plupart des propriétés des images astronomiques à courte exposition ne dépendront pas de manière significative de la taille précise de l'échelle extérieure (bien que l'amplitude du mouvement de l'image dépende encore faiblement de la taille de l'échelle extérieure).
À petite échelle ( <1cm), l'énergie turbulente de l'atmosphère est dissipée grâce à la viscosité de l'air (Roddier, 1981). L’échelle de longueur à laquelle cela devient significatif est appelée l’échelle interne de turbulence ( l0). L'inclinaison du spectre de turbulence de Kolmogorov signifie que toute réduction de puissance à de si petites échelles de longueur a relativement peu d'effet sur les performances d'imagerie des télescopes optiques et infrarouges.
La mesure de r0 est une façon
quantitative de mesurer la turbulence
Principe
La méthode consiste à mesurer les différences de pente du front d’onde sur deux petites pupilles distantes l’une de l’autre. Puisqu’il s’agit d’une méthode différentielle, la technique est intrinsèquement insensible aux erreurs de suivi. Elle avait déjà été utilisé dès 1960 pour fournir des estimations visuelles qualitatives. La théorie des mesures différentielles est désormais bien comprise. Elle montre que le mouvement différentiel dépasse le mouvement absolu dès que la distance entre les deux ouvertures est égale à quelques fois leur diamètre. Ainsi, un instrument compact peut être construit tout en offrant une bonne sensibilité. Il faut sélectionner la lumière des étoiles ayant traversé deux ouvertures circulaires dans le plan de la pupille d'entrée (trous Hartmann) de manière à obtenir des images d'étoiles dédoublées dont le mouvement relatif dans le plan image représente les inclinaisons locales du front d'onde. La théorie est passée en revue dans ce qui suit, les moniteurs type ESO et Hartmann sont décrits.
Principe de la mesure DIMM
ESO DIMM
La méthode de l'ESO afin de produire les deux images dans le plan focal, utilise un prisme dans l'un des trous de Hartmann pour dévier la lumière passant dans ce trou. Vous trouvez ci-dessous la théorie de l'ESO-DIMM.
L'ondulation du front d'onde z(x,y) est proportionnelle à l'erreur de phase du front d'onde : φ(x,y)
z(x,y)=λ/2π φ(x,y)
Puisque les rayons lumineux sont normaux à la surface du front d’onde, la composante α de la fluctuation de l’angle d’arrivée dans la direction x est donnée par :
α(x,y)=-∂z(x,y)/∂x= λ/2π ∂φ(x,y)/∂x
Ainsi, la covariance de la fluctuation de l’angle d’arrivée
Bα(ξ,η)=<α(x,y),α(x+ξ,y+η)>
est liée à la covariance de la fluctuation de phase Bφ(ξ,η) par :
Bα(ξ,η)=-(λ/2π)2 ∂2Bφ(ξ,η)/∂ξ2
en introduisant la fonction de structure de phase :
Dφ(ξ,η)=2[Bφ(0.0)-Bφ(ξ,η)]
cela devient donc :
Bα(ξ,η)=1/2(λ/2π)2 ∂2Dφ(ξ,η)/∂ξ2
Pour la turbulence de Kolmogorov à l'approximation du champ proche, la fonction de structure de phase est donnée par l'expression (3) largement utilisée :
Dφ(ξ,η)=6.88 (r/r0)5/3
où ro et est le paramètre de Fried. avec r=r0√(ξ2+η2)
Bα(ξ,η)=0.145λ2 r0-5/3 [(ξ2+η2)-1/6 -1/3ξ2(ξ2+η2)-7/6]
Avec η=0 on obtient la covariance longitudinale(dans le sens de l'inclinaison) en fonction de l'écartement ξ=d
Bα(d,0)=0.097 (λ/r0)5/3(λ/d)1/3 (9)
Pour ξ=0, on obtient le latéral ou covariance transversale (dans une direction perpendiculaire à l'inclinaison) en fonction de l'écartement η=d
Bα(0,d)=0.145 (λ/r0)5/3(λ/d)1/3 (10)
La covariance transversale est exactement 1,5 fois plus grande que la covariance longitudinale et les deux diminuent comme la puissance -1/3 de la séparation entre les trous. Cela a été bien confirmé expérimentalement par Borgnino et al. (1978). Ces expressions ne sont valables que dans la plage inertielle du spectre de Kolmogorov. La divergence à l’origine n’est clairement pas physique. En pratique, la valeur à l'origine est limitée par la moyenne d'ouverture et est donnée par l'expression de la variance du mouvement de l'image dérivée de Fried (1965, 1975) et Tatarski (1971), (avec un facteur deux puisque on considére le mouvement dans un seul sens) :
Bα(0,0)=0.179 (λ/r0)5/3(λ/D)1/3 (11)
où D est le diamètre des ouvertures à travers lesquelles les inclinaisons sont mesurées. En raison de la lente diminution de la covariance avec la puissance -1/3 de la distance, la moyenne de l'ouverture ne modifie pas sensiblement la fonction de covariance dès que la distance dépasse le double du diamètre de l'ouverture, comme indiqué ci-dessous. La variance du mouvement différentiel de l'image observée sur une distance d est donnée par : σ2(d)d
σ2(d)=2[B(0)-B(d)] (12)
En portant (9) et (11) dans (12) on obtient une expression approximative de la variance du mouvement longitudinal différentiel pour : σl2d>2D
σl2=2λ2r0-5/3[0.179D-1/3-0.0968d-1/3] (13)
alors que mettre (10) et (11) dans (12) donne une expression approximative de la variance , du mouvement transversal différentiel pour : σt2d>2D
σt2=2λ2r0-5/3[0.179D-1/3-0.145d-1/3] (14)
Ces variances peuvent être exprimées en termes de la variance totale σ pour un mouvement bidimensionnel à travers une seule ouverture de diamètre D:
σ2=2Bα(0,0)=0.358(λ/r0)5/3(λ/D)1/3 (15)
en utilisant (14) dans (12) et (13) avec S=d/D on obtient :
σl2=(1-0.541S-1/3 ) σ2
σt2=(1-0.811S-1/3 ) σ2
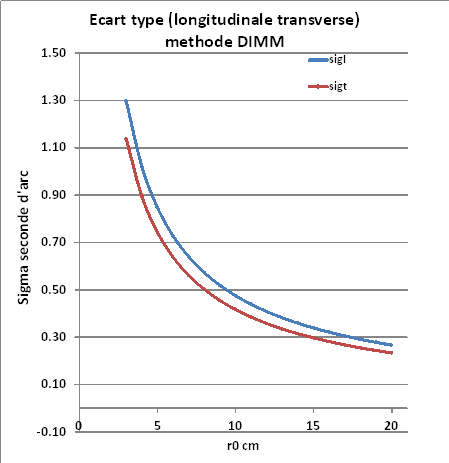
Les équations ci-dessus constituent la base de la méthode DIMM. Elles sont tracées ci dessous pour 2 ouvertures de 4cm espacées de 20cm

on calcul ro à partir de l'expressions (15) on a
σ2=Kλ2r0-5/3D-1/3 d'où:
r0=λ-6/5(σl,t2/Kl,t)3/5 D1/5 avec Kl=0.358 (1-0.541S-1/3) et Kt=0.358 (1-0.811S-1/3)
on a donc 2 mesures de r0 (qui doivent être cohérentes) en mesurant la distribution des déplacements différentiels longitudinaux et transversaux.
La méthode H-DIMM pour mesurer la turbulence astronomique est une modification de l'ESO-DIMM. Ainsi, toute la théorie mentionnée jusqu’à présent s’applique également aux deux méthodes. Dans le H-DIMM, les deux images sont produites par un simple masque de Hartmann, sans prisme. Donc ici, on étudie l'influence de la défocalisation du télescope, puisque pour le calcul de la valeur de la turbulence à travers le mouvement différentiel de l'image, les mêmes équations sont utilisées.
L'élimination du prisme de séparation d'image est possible car la profondeur de champ des sous-ouvertures est beaucoup plus grande que celle du système optique parent. Pour un diamètre d'ouverture D, une longueur d'onde λ et une distance focale f , la profondeur de champ est donnée par :
2ΔZ=1.22λ(f/D)2
Par conséquent, si le CCD d'imagerie est décalé d'une certaine quantité par
rapport à la meilleure mise au point <ΔZ(soit à l'intérieur, soit à l'extérieur
de la meilleure mise au point), alors la fonction d'étalement de points produite par
chaque sous ouverture sera impossible à distinguer des images de sous ouverture
parfaitement focalisées. Cependant, les images produites par des sous ouvertures
séparées par une distance d
deviennent bien séparées lorsque :
Δz=1.22λ(f/d)2
Lorsque le détecteur est situé à distance Z du plan focal du télescope imageur, où , toutes les images d'une étoile produites par des sous-ouvertures plus séparées les unes des autres seront bien séparées dans le plan image et seront parfaitement mises au point. Dans ces circonstances, le mouvement différentiel de l'image est facile à déterminer à partir des fluctuations des centroïdes de chaque image d'une exposition à l'autre. il faut Δz<Z<ΔZd
Un rapport optimal entre la séparation des images et le diamètre est obtenu en plaçant le détecteur à la mise au point telle que Z≈ΔZ
Exemple : ouvertures de 5cm avec une distance entre les ouvertures d=40cm. focale du télescope f=250cm
de focalisation optimum: ΔZ=0.66 5e-4 (250/5)2 = 0.8mm
séparation des images à partir de Δz=1.22 5e-4(25/4)2 =0.02mm
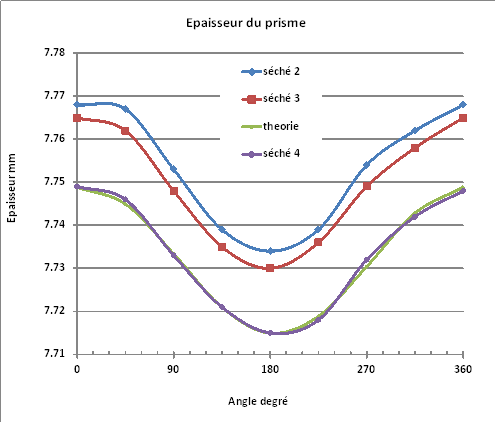
Réalisation du prisme
j'ai découpé au biscuit cutter dans de la glace de St Gobain 2 rondelles de 82mm de diamètre .
La déviation donnée par un prisme de petit angle est (n-1)A ou A est l'angle du prisme. Pour un angle de 1.5 minute cela donne une déviation de l'ordre de 45" ce que j'ai choisi. Sur 80mm la différence d'épaisseur entre le coté mince et épais du prisme est de 35µm. Cet angle est très facile à obtenir avec quelques séchées