Correction de l'astigmatisme résiduel d'un miroir mince au moyen de son barillet
2) Génération d'astigmatisme au moyen de forces
4) Dispositifs de compensation
Un des problèmes des grands miroirs minces des amateurs est l'astigmatisme. Au niveau des télescopes professionnels, l'astigmatisme est compensé périodiquement au moyen des actuateurs du barillet en fonction de la position du télescope. Cette correction dynamique qui nécessite l'analyse du front d'onde est difficile à réaliser au niveau amateur par contre on peut envisager une correction statique qui améliore la forme du miroir. Cette correction doit être intégrée au barillet du miroir et pour être efficace ne pas nécessiter de réglages fréquents. Disposant de 2 miroirs de 500mm dont l'un accuse un astigmatisme résiduel non complètement corrigé j'ai modifié le barillet de mon télescope de 500mm pour y intégrer un dispositif de correction de l'astigmatisme. Évidemment l'idéal est d'avoir un miroir dépourvu d'astigmatisme mais le dispositif décrit ci dessous permet d'améliorer les images provenant d'un miroir astigmate.
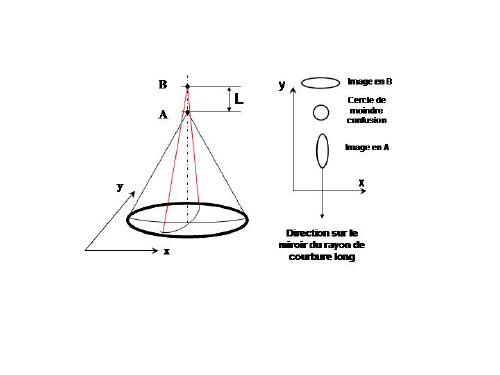
L'astigmatisme sur l'axe d'un télescope s'il est du au miroir primaire provient du fait que la surface du miroir n'est pas de révolution mais présente deux rayon de courbures orthogonaux différents. Dans ces conditions les rayons lumineux sont focalisés dans deux plans différents. La distance L entre ces plan est la longueur d'astigmatisme.
Sur la figure ci dessus le grand rayon de courbure est suivant Y
L'image d'un point observée avant le foyer (intra focale) est une ellipse dont le grand axe est dirigé suivant le grand rayon de courbure R1. Lorsque l'on se rapproche du foyer, l'excentricité de l'ellipse diminue pour devenir un cercle. On est au meilleur foyer (c'est la position du cercle de moindre confusion) mais la tache obtenue peut avoir un diamètre notablement plus important que la tache de diffraction théorique. Son diamètre dépends de l'ampleur de l'écart entre les deux rayons de courbure. Lorsque l'on s'éloigne du foyer (extra focale) on retrouve une ellipse dont le grand axe a tourné de 90° et dont la direction est celle du petit rayon de courbure du miroir R2.
André Couder a donné les limites acceptables pour l'astigmatisme [24].
Soit ε la mesure de l'astigmatisme sur l'onde qui s'exprime en fonction des rayons de courbure R1 et R2 de la surface par:
ε = (h2/2)(1/R1-1/R2)
ε = (Φ2/8)(1/F-1/(F-L))=(L/8)(Φ/F)2 (1)
Ou Φ est le diamètre du miroir et F=R/2 est sa focale.
L est la longueur d'astigmatisme
Si ε=λ/6.5 l'astigmatisme est indétectable (Couder) [24], λ est la longueur d'onde de référence (0,56µm)
Si ε=λ/4 l'astigmatisme est décelable par image parfaite mais il n'affecte pas le pouvoir séparateur.
Au delà le pouvoir séparateur est dégradé. La mesure pratique de l'astigmatisme se faits en mesurant L qui est 200 fois plus important que ε pour un miroir ouvert à F/Φ=5.
L'écart εv tolérable sur le verre est la moitié de la valeur calculée sur l'onde.
2) Génération d'astigmatisme au moyen de forces.
La déformation d' une plaque circulaire correspondant à un astigmatisme pratiquement pur peut être généré au moyen de 4 forces P de même intensité appliquées sur deux axes perpendiculaires de la plaque suivant l'arrangement suivant:
La déformation de la plaque est donnée par [22][23]:
w(ρ,θ)=Pa2/(π(3+ν)D)( ∑ [1/m(m-1)+2(1+ν)/((1-ν)(m-1)m2)-ρ2/(m(m+1))]ρmcos(mθ)) (2)
la somme ∑sur m est prise pour m=2*(2k+1) 0<=k<∞ soit m=2,6,10....
D=Ee3/(12(1-ν2)) est la rigidité de la plaque
e est l'épaisseur de la plaque, a=Φ/2 est le rayon de la plaque et 0<= (ρ=r/a) <=1
E est le module d'Young et ν est le coefficient de Poisson de la plaque
Le terme prépondérant de la série (2) est le terme correspondant à m=2, le terme d'après pour m=6 est faible environ 3% du terme précèdent.
Le terme en ρ2 dans le crochet est l'écart à un astigmatisme pure ρ2 cos(2θ). Cela représente l'erreur induite par la méthode
Ce terme est maximum et vaut 1/6 à la périphérie du miroir alors que le coefficient constant vaut 1/2+1/2 (1+υ)/(1-υ) ≈ 1.3
On induit donc une erreur de méthode de 1/6/1.3 ≈ 0.12
Si la surface présente un astigmatisme de λ sur la surface la correction fournira une surface avec un astigmatisme résiduel de λ/8
On peut donc corriger de cette façon une surface présentant un astigmatisme de 1.25 à 1.5λ pour qu'elle satisfasse au critère de Couder
On peut calculer la valeur de l'astigmatisme ε induit par cet arrangement de forces. On a
ε mécanique= w(a,0)-w(a,π/2)
ε mécanique onde = [48 P a2(1-ν2)/((3+ν)πEe3)]*(1/3+(1+ν)/(2(1-ν))) ≈ 5.07 Pa2/Ee3 (3)
En appliquant les forces positives perpendiculairement à l'axe du grand rayon de courbure du miroir R1 et les forces négatives sur l'axe du petit rayon de courbure R2 avec une intensité telle que ε mécanique= ε on doit corriger l'astigmatisme avec une bonne précision.
La longueur d'astigmatisme générée est :
L mécanique=8 (F/Φ)2 ε mécanique
Pour du verre E=7,27 1010 Pa et ν=0.23
Dans le cas de mon miroir de 500mm on a e=0.04m et a=0.25m on en déduit en appliquant la formule (3) que
ε mécanique onde = 68nm/N
On voit que 4 forces P de 10N (1kg) suivant l'arrangement décrit permettent de corriger 680/560 ≈ 1.2 λ d'astigmatisme sur l'onde.
On voit également toute la sensibilité du miroir à l'astigmatisme et la nécessité de pouvoir régler les forces avec une précision de quelques dizaines de grammes.
Pour un miroir de 300mm de diamètre et de 40mm d'épaisseur ε mécanique onde = 25nm/N. Un tel miroir est beaucoup moins sensible à l'astigmatisme induit par son barillet ou par un travail sur un poste non parfaitement plan, il sera également plus difficile à compenser car les forces à appliquer peuvent devenir importantes.
Pour un miroir de 600mm ε mécanique onde = 98nm/N la limite de Couder est atteinte pour une force de l'ordre de 1N.
On se limitera à des déformation de l'ordre de λ/2 (sur la surface) en suivant ce que dit Gérard Lemaitre dans sa thèse [36]:
"Lorsque des miroirs travaillant dans des systèmes optiques centrés de bonne qualité, présentent de l'astigmatisme en fournissant des images relativement elliptiques sur l'axe, il est possible d'éliminer ce défaut (généralement dut à une mauvaise assise du miroir lors de la taille) en exerçant directement sur le miroir des forces égales et opposées suivant deux diamètres principaux d'astigmatisme. Toutefois, ce procédé ne saurait être efficace si la déformation est supérieure à une demie longueur d'onde, car
1° La déformation radiale n'est pas purement en ρ2 ( cf équation (2)), surtout pour des miroirs concaves ayant leur face arrière plane.
2° La répartition angulaire de la déformation en cos2θ, engendrée uniquement par les quatre points, est plus facile à respecter, mais peut produire des déformations locales gênantes au voisinage des quatre zones d'appuis."
Le dispositif décrit peut être appliqué à un barillet composé de supports triangulaire. Pour de grands miroirs, les barillets avec des supports triangulaires ne sont pas idéaux car les appuis latéraux peuvent engendrer des couples importants générateur d'astigmatisme. La raison principale de cet astigmatisme est la distance entre le point d'appuis latéral et le point fixe sous le miroir cf figure ci dessous.
Pour éviter largement ces problèmes un barillet avec des leviers astatiques et des points fixes proche des contacts latéraux est bien meilleur. Par ailleurs il est également possible d'optimiser la forme du miroir (notamment l'aberration sphérique) si plusieurs couronnes de leviers sont utilisées.
Mon barillet est constitué de 12 points repartis sur deux couronnes de leviers une au bord et une sur un rayon de 0.33 Rmiroir.
La première couronne extérieure est constituée de 9 points dont 3 points "fixes" (des vis) permettant de régler la position du miroir et 6 leviers. La deuxième couronne est constituée de 3 leviers, en modifiant la charge respective des couronnes il est possible de modifier l'aberration sphérique du miroir.
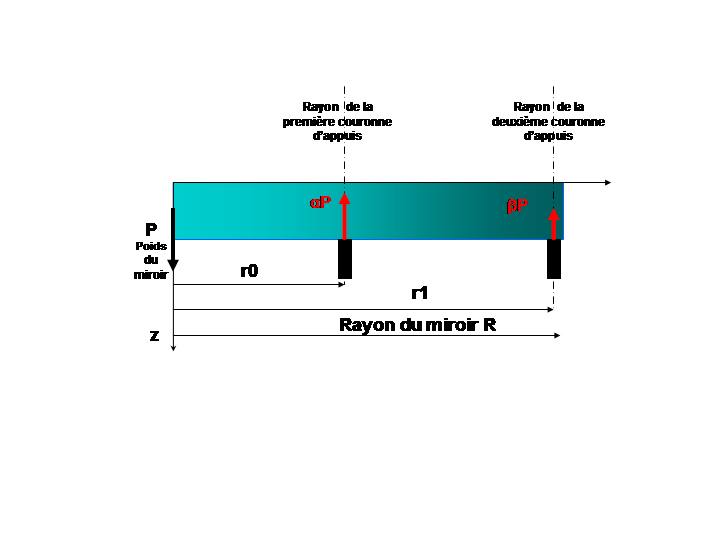
André Couder [24] [25] a donné les formules permettant de calculer la déformation d'un miroir en fonction de la charge affectées aux diverses couronnes supportant le miroir.
La déformation z d'un miroir en appuis sur une couronne de rayon ro est donnée par:
z(ξ)=3/4 (1-ν2) (gδ/E2) (R4/e2) (1/4V-U) =K (V/4-U)
ξ étant la coordonnée radiale normalisée (ξ=r/R) d'un point du miroir et ρ0=ro/R
K=3/4 (1-ν2) (gδ/E2) (R4/e2)
V et U valent :
V=ξ4 - (6+2ν)/(1+ν) ξ2 + (5+ν)/(1+ν)
U=2(1-ρ2)+(1-ν)/(1+ν)(1-ξ2)(1-ρ2)+2(ξ2+ρ2)log(ρ) pour 0<ξ<ρ
U=2(1-ξ2)+(1-ν)/(1+ν)(1-ξ2)(1-ρ2)+2(ξ2+ρ2)log(ξ) pour ρ<ξ<1
Pour un miroir supporté par deux couronnes de rayon ro et r1 portant des charges respectives α =Po/Pmiroir et β=1-α on a:
z(ξ ,ρ0, ρ1)=K [1/4V(ξ)-αU(ξ, ρ0)-(1-α)U(ξ, ρ1)] (4)
Pmiroir est le poids du miroir
La formule se généralise s'il y a plus de deux couronnes d'appuis avec des charges respectives α, β, γ, ... avec
α+β+γ+ ... =1
On optimise donc les charges et la position des couronnes pour minimiser z. Chaque couronne est constituée d'un multiple de 3 points d'appuis (leviers astatiques et points fixes pour la couronne extérieure).
Dans le cas d'un miroir parabolique il est important de supprimer l'aberration de sphéricité introduite par la déflexion du miroir sous son poids. Cette aberration est représenté par le terme en ξ4 dans la formule (4). Il peut subsister une légère courbure (terme en ξ2) qui ne nuit pas à la qualité optique et qui ne fait qu'entraîner une légère modification de la focale.
La feuille de calcul permettant de calculer la masse et la position des leviers pour un barillet comportant jusqu'à 3 couronnes est ici.
Les vues générales du barillet réalisé coté pile et face sont présentées ci dessous. Je décrirais le dispositif de correction de l'astigmatisme un peu plus loin. Le fond du barillet est réalisé en tube carré de 30mm soudés entre eux pour éviter d'avoir à faire à une pièce massive longue à mettre en température. Compte tenue de l'épaisseur des tubes, le fond est très rigide. La découpe des tubes est définie par l'emplacement des 12 points de soutient du miroir.
barillet: à gauche coté miroir à droite coté leviers
Les leviers astatiques sont réalisés simplement. Un axe en acier inoxydable de 10mm de diamètre est logé dans deux paliers constitués par des roulements à billes. Le corps du levier est en aluminium prolongé par une tige fileté de 10mm sur laquelle la masselotte servant à établir la force sous le miroir est visée. Le réglage précis de la force est réalisé en déplaçant la masselotte sur cette tige. Les masselottes sont réalisées en bronze dans un rond de 30mm de diamètre
leviers astatiques
Les douilles dans lesquelles coulissent les butées sont en aluminium et les butées sont en acier inox polies pour avoir le minimum de friction. Aucun graissage n'est souhaitable car en vieillissant la graisse ou l'huile bloque le système. Une vis de réglage (en bleu sur la figure ci dessus) sur le corps du levier permet d'amener les leviers dans un plan parallèle au fond du barillet.
Aux douze points du barillet, 4 forces pour modifier l'astigmatisme ont été rajoutées au moyen de 2 dispositifs poussant et de deux tirants. Contrairement aux leviers astatiques qui doivent fournir une force d'appuis variant avec l'inclinaison du miroir la correction de l'astigmatisme inhérent au miroir doit être réalisée par des forces indépendantes de l'orientation du télescope. Ces forces sont fournis par des ressorts.
4) Dispositifs de compensation de l'astigmatisme
la figure ci dessous représente les dispositifs de compensation permettant de générer les forces correctrices.
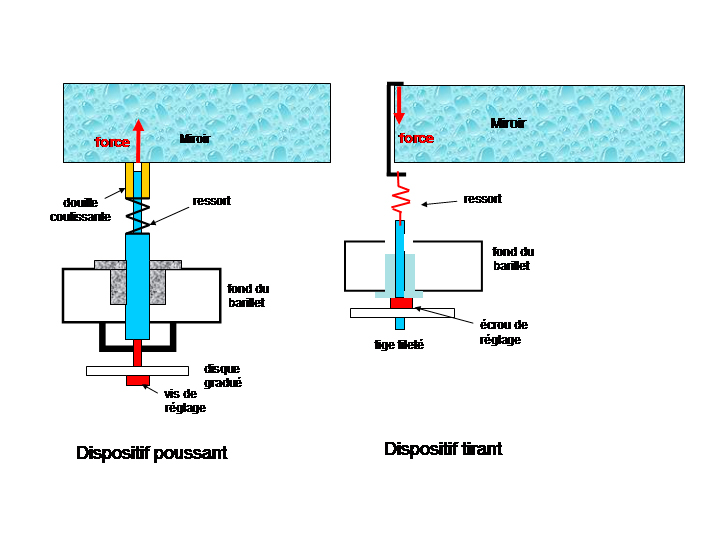
Dispositif poussant (image de gauche)
La force est définie par la compression d'un ressort monté sur un piston terminé par une douille coulissante. Le piston est déplacé au moyen d'une vis graduée. lorsque l'on fait monter le piston la douille ne bouge pas car elle est en appuis sur le dos du miroir donc on comprime le ressort et on augmente la force poussant le dos du miroir.
Dispositif tirant (image de droite)
La force est définie par la tension d'un ressort monté sur un crochet en appuis sur la face avant du miroir. Le ressort est tendu au moyen d'un écrou gradué qui se visse sur une tige fileté reliée au ressort. Lorsque l'on fait descendre la tige filetée la tension du ressort augmente et la force tirant la face avant du miroir augmente.
On voit qu'une rotation identique des vis de réglage induit des forces tirant et poussant identiques si les ressorts des deux dispositifs ont la même rigidité. Ce qui est le cas.
Les deux types de dispositifs sont installés sur deux axes perpendiculaires hors des plots du barillet cf photos.
Il faut d'abord orienté les axes d'astigmatisme du miroir correctement par rapport aux quatre points de compensation c'est à dire grand rayon de courbure R1 aligné sur les dispositifs poussant et petit rayon de courbure R2 suivant les dispositifs tirant.
On règle ensuite l'inclinaison du grand miroir et les leviers astatiques pour centrer correctement l' image d'une étoile, l'étoile étant proche du zénith.
On doit voir les ellipses caractéristiques d'une image astigmate avec les axes orientés suivant les axes de compensation.
On amène les plots de compensation poussant en contact avec le dos du miroir et on visse les écrous pour avoir une force tirant nulle (ou proche de zéro).
On vis les 4 vis de réglages (2 vis et deux écrous) d'une même angle. L'astigmatisme de l'image doit diminuer. On continue le processus jusqu'à annuler l'astigmatisme.
On optimise le centrage des miroirs et on retouche l'astigmatisme si nécessaire.
L'astigmatisme ne doit pas évoluer avec le changement d'inclinaison du télescope.
Au niveau du réglage le miroir plan peut jouer des tours s'il est lui même astigmate. Il faut commencer par tourner le primaire dans son barillet pour minimiser l'astigmatisme.
Dans mon cas, après rotation du primaire j'ai réussi à compenser l'astigmatisme résiduel. J'ai fait le réglage en visuel en intra et extra focal. J'ai rendu l'image bien circulaire à l'oculaire sachant que la turbulence ne me permet pas de voir la figure de diffraction.
La PSF du télescope après réglage prise avec 6m de focale, des pixels de 2.9µm et un filtre IR qui coupe à 650nm est ci dessous:

PSF
Le premier anneau fait 23µm de diamètre environ
il subsiste quelques problèmes de coma et de trèfle à corriger
© Jean DIJON : Tous les documents présents
sur ce site sont protégés par les lois sur les droits d'auteur.
La reproduction et la diffusion de ces documents sont interdites sans le consentement de l'auteur.