Bruit et magnitude limite des images CCD
Bruit engendré par le fond de ciel
Un certain nombre de d'amateurs ont du mal à s'y retrouver dans la jungle des flats, darks et se posent beaucoup de questions sur la meilleure acquisition à faire pour ces images de références. Pour comprendre la logique et optimiser sa technique, il faut revenir au point fondamental qui est le rapport signal sur bruit de l'image.
En préalable rappelons qu'une image brute CCD ou sortant d'un APN est entachée d'erreur que l'on peut et doit corriger ce qui permet d'obtenir des résultats inégalables par les techniques de photographie classique. Un CCD est composé d'une matrice de pixels dont le rôle est de transformer les photos incidents en électrons. Ces électrons lus par l'électronique du système sont convertis en une grandeur numérique qui représente un niveau de gris de l'image.
Les problèmes surgissent car il y a une autre source d'électrons dans le capteur que les photons incident à savoir une génération thermique d'électrons. Ce signal thermique augmente avec le temps. On a donc après l'acquisition d'une image pour chaque pixel (X,Y) un nombre d'électrons Nbrut qui vaut:
![]() (1)
(1)
L'image étant numérisée, on peut faire des calculs pour retrouver le nombre de photons incident (ce qui nous intéresse). On se dit qu'il "suffit" de retrancher Nthermique à Nbrut pour retrouver notre information. Pour déterminer Nthermique il faut donc faire une deuxième image dans les mêmes conditions que la première sans ouvrir l'obturateur pour que Nphoton soit nulle. Cette image que l'on nomme "Noir" ou "Dark" contient un nombre d'électrons qui n'est malheureusement pas rigoureusement identique à Nthermique à cause du bruit présent dans le système. Par ailleurs Nthermique n'est pas constant en fonction des coordonnées X,Y des pixels. Lorsque l'on soustrait Nthermique on va supprimer les inhomogénéités pixel à pixel mais il va rester du bruit.
Le bruit à plusieurs origines. Pour Nphotons il provient du fait que les photons arrivent au hasard sur le capteur avec en moyenne un flux donné qui est celui de l'étoile observé. Donc pour deux poses de durées identiques, le nombre de photons incidents n'est pas identique mais fluctue en suivant une statistique de Poisson. Cette statistique a un écart type σ qui est égal à la racine carrée de la valeur moyenne (signal) :
![]() (2)
(2)
avec S le signal intéressant et B le bruit. Lorsque l'on a plusieurs sources de bruit B1, B2 le bruit s'ajoute de façon quadratique c'est a dire que l'on a
![]() (3)
(3)
Le signal thermique peut s'écrire en fonction du temps de pose t et de la température T au moyen d'une équation du type
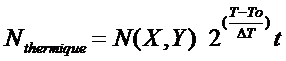 (4)
(4)
ou ΔT est l'écart en température pour obtenir un doublement du courant noir et To est la température ambiante. N(X, Y) représente le nombre d'électrons générés par seconde dans le pixel X, Y à la température ambiante.
Si on reprend l'équation (1) correspondant à l'image non traitée le bruit dans cette image est :
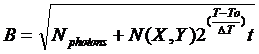 (5)
(5)
le premier terme représente le bruit de photons et le deuxième terme le bruit du courant noir
Notre image équation (1) comporte un signal parasite N1thermique (t1) qu'il faut soustraire pour retrouver l'image en provenance du ciel.
Si on soustrait le signal thermique obtenue lors de l'acquisition du noir pris à l'instant 2 on a donc:
![]()
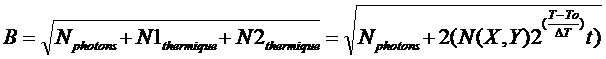
Ces équations montrent que l'on a bien traité l'image c'est à dire que l'on a bien récupéré le signal utile S mais on a également augmenté le bruit d'un facteur 2 (le bruit s'additionne toujours et ne se retranche jamais même quand on soustrait deux images).
On voit bien ici tout l'intérêt des cameras refroidis de façon importante pour diminuer la contribution du bruit thermique et donc le bruit dans l'image traitée
Pour faire mieux au niveau du traitement il faut diminuer le bruit dans l'image Noire. Comment et ce possible?
Pour cela, il faut moyenner des images noires identiques. En effet, si j'additionne m images "identiques", mon signal utile est multiplier par m alors que mon bruit est multiplier par racine (m). Le rapport signal sur bruit qui mesure la qualité de l'image est augmenté d'un facteur racine (m)
![]()
![]()
Comme nous voulons soustraire un signal correspondant au signal thermique présent dans l’image brute il faut diviser la somme des images noires par m (faire la moyenne) on a donc:
![]()
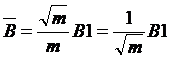
dans ce cas si on soustrait le dark moyen B à l’image brute le bruit vaut :
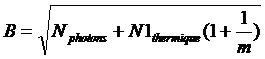 (7)
(7)
Si on fait la moyenne d'une dizaine de "dark" le bruit dans l'image n'augmente plus que de 10% par rapport à l'image originale, on a pas perdu grand chose au niveau bruit et on a fortement amélioré l'image.
Le seul inconvénient de cette méthode c'est la nécessité de faire une dizaine de darks alors que l'on pourrait utiliser le temps utile pour faire des observations. Pour éviter cette perte de temps il faut posséder une camera stabilisée en température et toujours travailler à la même température lors des prises d'images. On réalise alors ce que l'on appel un "noir maître" qui nous servira à traiter l'image.
Il nous faut revoir un peu notre équation (4) qui décrit la génération thermique des électrons pour être plus proche de la réalité. En effet cette équation nous dit que le courant noir est nul pour un temps d'exposition nul mais en réalité, on mesure un signal non nul que l'on appel l'offset. On a en donc:
![]() (8)
(8)
Si on fixe la température du capteur, on vas pouvoir calculer le courant noir pour un temps de pose t2 donné du moment que l'on a mesuré Noffset et que l'on a mesuré le courant noir pour un temps de pose t1 connu . En effet on a pour un temps t2 quelconque:
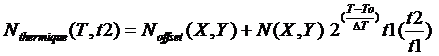 (9)
(9)
on appel noir maître ("master dark") la partie dépendante du temps
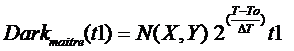
si on connais cette image à l'avance on peut calculer le courant noir pour n'importe quel temps d'exposition avec l'équation (10) ci dessous
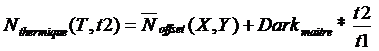 (10)
(10)
Évidemment on a moyenné ces images sur un grand nombre (p) d'images élémentaires pour diminuer le bruit du noir maître.
=============================================================================================================
En résumé:
on fait à la température d'utilisation de la camera
1) p images obturateur fermé avec un temps de pose nulle et on calcul l'offset moyen :
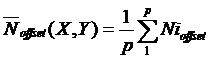 (11)
(11)
2) p images obturateur fermé avec un temps de pose t1 qui doit être au moins égal au temps de pose le plus long envisagé, et on calcul le noir maître:
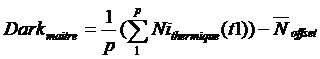 (12)
(12)
Typiquement p doit être de l'ordre de grandeur du nombre d'images élémentaires que l'on souhaitera additionner dans l'image finale (voir plus bas).
============================================================================================================
Si on revient à l'équation du bruit on a après traitement, en considérant que le bruit de l'offset est le bruit de numérisation de l'image Nnum (constant), un bruit:
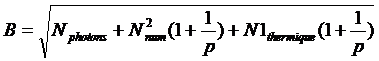 (13)
(13)
Le rapport signal sur bruit R qui mesure la qualité de l'image est donc
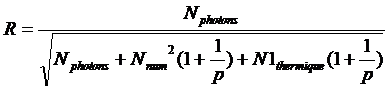 (14)
(14)
Pour beaucoup de raisons (guidage, saturation du capteur...) il est intéressant de fractionner une pose longue en poses plus courtes et d'additionner les images obtenues dans l'ordinateur. On peut ainsi trier les images et éliminer les images bougées par exemple, éviter les problèmes de blooming... par contre il ne faut pas faire n'importe quoi au niveau du traitement sous peine de voir ses efforts ruinés.
Supposons que l’on ait pris deux images du même objet mais que par lassitude on ait pris qu’un seul noir correspondant au temps de pose d’une des images et que l’on se propose de soustraire deux fois le même noir
On a bien au niveau de l’image brute
![]()
Au niveau de l’image traitée
![]()
Mais au niveau du bruit on a
![]()
En effet on a utilisé dans le traitement deux fois le même noir donc le bruit est multiplié par 2 contrairement au cas d’images (de noirs) indépendantes
qui dans ce cas donneraient
![]()
Le rapport signal sur bruit vaut alors
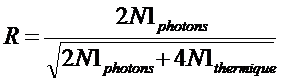
Soit en posant x=N1thermique/N1photons et M le rapport signal sur bruit que l’on aurai eu si on avant fait les deux noirs
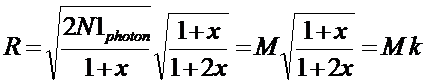
La formule se généralise au cas d’un plus grand nombre d’images. Les courbes suivantes montrent le résultat de ce traitement simplifié dans le cas de l’addition de plusieurs images pour un rapport S/B de 1 donc par exemple pour une étoile que l’on voudrait voir apparaître après addition des images. On voit pour ce cas extrême la perte associée à ce traitement. On n’a pas mieux en additionnant 9 images qu’avec 3 convenablement traitées. Si le rapport signal sur bruit de l'objet est plus fort la perte est moindre. Le résultat est trompeur, car pour les fortes illumination la perte est faible. On perd essentiellement dans les basses valeurs donc en détectivité. En conclusion faire des noirs n’est pas un luxe il vaut mieux additionner convenablement un peu moins d’images que de ne pas faire suffisamment de noirs.
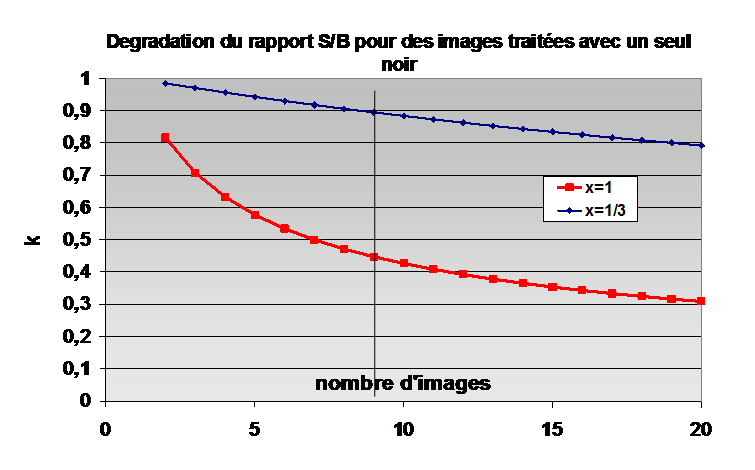
Dégradation du rapport S/B pour une somme d'images traitées avec un seul noir par rapport au traitement correct. En rouge pour la limite de détectivité . En bleu pour une forte illumination. le traitement correcte donne k=1
L’analyse présentée ci-dessus est trop simpliste car en fait un bruit sournois dont nous n’avons pas encore parler viens atténuer un peu les conclusions précédentes. Il s’agit du bruit du fond du ciel. Le fond de ciel agit comme une source parasite et même si on peut atténuer ses effets et faire des images impensable en photos argentiques le problème viens du bruit de photons engendré par cette source parasite.
4) Bruit engendré par le fond de ciel
En repartant de l’équation (13) pour une image correctement traitée on a simplement pour le bruit un terme supplémentaire Nciel donc
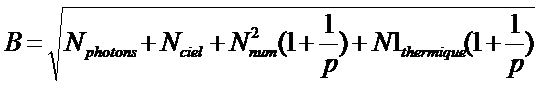 (15)
(15)
Le signal brut est
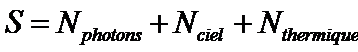
Si maintenant on a fractionné la pose totale en k poses élémentaires posées un temps
t1= total /k on a un bruit :
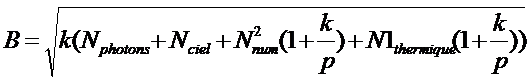 (16)
(16)
Voyons sur des exemples ce que cela veut dire concrètement.
Avant cela il nous faut établir un modèle complet du CCD.
Suivant la qualité de son site le fond de ciel vas avoir une brillance exprimée en magnitude par seconde carrée qui vaut typiquement:
|
Site |
Brillance fond de ciel mg sec-2 |
|
Observatoire |
22.5 |
|
Site de montagne |
20_21 |
|
Site de plaine |
18_19 |
|
Site banlieue urbaine |
16_17 |
|
Site en ville |
15_16 |
Il nous faut calculer le nombre de photons incident en provenance de l’étoile. Pour ce faire, on calcul le flux de photons par cm2 pour une étoile de référence de magnitude 0. Après cela on utilise la formule de Pogson qui permet de calculer le flux F2 pour une étoile de magnitude quelconque. On a:
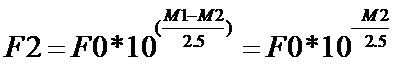 si M1=0 (17)
si M1=0 (17)
Pour déterminer F0 on utilise les données fournies par C. Buil [12]
On a
|
Longueur d’onde |
F0 (lambda) |
Ta Transmission Atmosphère |
|
4000 |
544 |
0.54 |
|
4500 |
873 |
0.63 |
|
5000 |
999 |
0.69 |
|
5500 |
1069 |
0.72 |
|
6000 |
1109 |
0.74 |
|
6500 |
1077 |
0.78 |
|
7000 |
1050 |
0.81 |
|
7500 |
1002 |
0.82 |
|
8000 |
958 |
0.79 |
|
8500 |
895 |
0.80 |
|
9000 |
851 |
0.86 |
|
9500 |
811 |
0.93 |
|
10000 |
755 |
0.97 |
F0 représente le flux de photons incident hors atmosphère. Au niveau de la mer on doit multiplier ce flux par la transmission de l’atmosphère Ta (λ) à la longueur d’onde donnée. Pour transformer ce nombre de photons en nombre d’électrons dans le détecteur on doit multiplier ce nombre par le rendement quantique du détecteur et par le facteur de transmission du filtre Tf (λ) si on en utilise un. Donc finalement
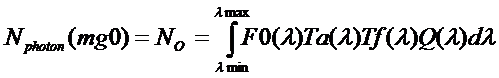 (18)
(18)
Pour le flux d’électrons Nciel en provenance du ciel de magnitude Mciel à travers le même système on a :
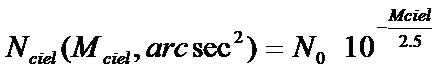 (19)
(19)
On a donc pour un télescope de diamètre D d’obstruction centrale d et de coefficient de réflexion r1 pour le primaire et r2 pour le secondaire un nombre d’électrons générés dans le capteur pour une étoile de magnitude Me
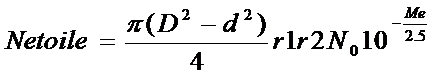 (20)
(20)
On a presque fini notre calcul. Il faut encore évaluer le nombre d’électrons généré dans un pixel. Pour l’étoile cela va dépendre de la turbulence. On montre que le profil stellaire peut être approximé spatialement par une gaussienne que l’on écrit:
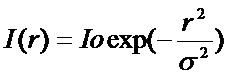
la largeur à mis hauteur (FWHM) du profil vaut
![]()
La largeur ne peut pas être inférieure à celle donnée par la diffraction qui vaut σmin = 0.618 λ F/D
Un pixel de taille Lp sous tend un arc xp exprimé en seconde d’arc
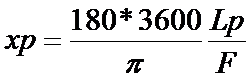 (21)
(21)
F étant la focale du télescope dans la même
unité que Lp (mm)
Le nombre maximum d’électrons générés dans un pixel de taille xp, yp en seconde
d’arc (si le pixel est carré xp=yp) est :
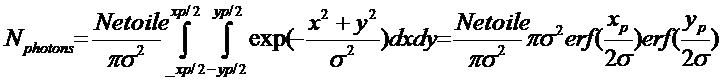
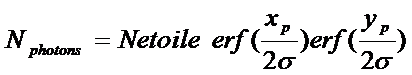 (22)
(22)
Le nombre d’électrons en provenance du ciel générés dans le pixel est
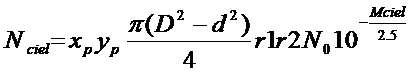 (23)
(23)
En regroupant ces équations on obtient un modèle de camera CCD qui permet de déterminer la détectivité de son couple télescope camera dans un site donné
Le modèle actualisé se trouve regroupé dans une feuille de calcul Excel que l'on peut charger ici feuille de calcul CCD
Les données à rentrer sont grisées: on a trois groupes de données
_les caractéristiques du télescope:
diamètre du primaire
diamètre du secondaire
coefficients de réflexions des miroirs
focale
_les caractéristiques du CCD (ou CMOS) et du traitement réalisé
Le bruit de lecture en e
Le courant noir en e par seconde
La taille des pixels en microns
Le facteur de binning
Le nombre d'images dans le noir maître ou le nombres de noirs indépendants utilisés pour traiter la pose
Le nombre de prises de vues dans la pose (fractionnement) ce coefficient est appliqué à tout le tableau même pour les poses courtes.
_les caractéristiques du site d'observation
Magnitude du fond de ciel
Turbulence
Altitude (joue sur la transparence)
La hauteur du champ observé (joue sur la turbulence et la masse d'air)
| Modèle CCD | ||||
| http//www.jeandijon.com | ||||
| télescope | ||||
| diamètre du miroir primaire | 50 | cm | ||
| diamètre du miroir secondaire | 10 | cm | ||
| coef de réflexion du primaire | 0,92 | |||
| coef de réflexion du secondaire | 0,96 | |||
| focale du télescope | 1825 | mm | ||
| rapport F/D | 3,65 | |||
| surface équivalente télescope | 1664,79 | cm2 | ||
| flux étoile mag0/cm2 | 884368,3313 | e/s | ||
| flux étoile mag0 | 1472287554 | e/s | ||
| CCD | ||||
| bruit de lecture | 10 | électrons | ||
| courant noir | 1 | électrons s-1 | ||
| taille des pixels | 18 | µm | ||
| nombre d'images dans le dark | 1 | |||
| nombre d'images dans la pose | 1 | |||
| sigma | 1,501 | sec |
|
|
| largeur des pixels en sec arc | 2,034 | sec | ||
| surface pixel | 4,137 | sec2 | ||
| xp/2/sigma | 0,6775 | |||
| %énergie étoile dans le pixel | 0,4334 | % | ||
| Site | ||||
| magnitude fond de ciel | 17 | mag sec-2 | ||
| turbulence | 2,5 | seconde d'arc | ||
| altitude | 400 | mètres | ||
| diamètre étoile | 0,022 | mm | ||
|
|
un tableau dans la même feuille cf ci dessous permet de rentrer le rendement quantique de son détecteur et la transmission du filtre utilisé s'il y en a
| lambda | N | Transmission Atmosphère | transmission filtre | rendement quantique | T(h) | NQFT | h(l) | ||
| 4000 | 544 | 0,54 | 1 | 0,02 | 0,566 | 6,15808 | 5200 | ||
| 4500 | 873 | 0,63 | 1 | 0,07 | 0,656 | 40,08816 | 4500 | ||
| 5000 | 999 | 0,69 | 1 | 0,17 | 0,714 | 121,2586 | 4300 | ||
| 5500 | 1069 | 0,72 | 1 | 0,23 | 0,743 | 182,6814 | 4200 | ||
| 6000 | 1109 | 0,74 | 1 | 0,25 | 0,766 | 212,3735 | 3500 | ||
| 6500 | 1077 | 0,78 | 1 | 0,29 | 0,802 | 250,4887 | 3500 | ||
| 7000 | 1050 | 0,81 | 1 | 0,3 | 0,83 | 261,45 | 3500 | ||
| 7500 | 1002 | 0,82 | 1 | 0,24 | 0,839 | 201,7627 | 3400 | ||
| 8000 | 958 | 0,79 | 1 | 0,24 | 0,812 | 186,695 | 3400 | ||
| 8500 | 895 | 0,8 | 1 | 0,2 | 0,821 | 146,959 | 3400 | ||
| 9000 | 851 | 0,86 | 1 | 0,15 | 0,875 | 111,6938 | 3400 | ||
| 9500 | 811 | 0,93 | 1 | 0,07 | 0,938 | 53,25026 | 3400 | ||
| 10000 | 755 | 0,97 | 1 | 0,04 | 0,973 | 29,3846 | 3400 | ||
|
|
la feuille calcule le rapport signal sur bruit (S/B) pour des étoiles de magnitudes données et pour des temps de pose échelonnés en fonction des données d'entrées (voir ci dessous)
Un objet est à la limite de détection quand sont rapport S/B est de 3
| pose | 1s | 10s | 1min | 10min | 1h | 5h | ||
| magnitude | 1 | 10 | 60 | 300 | 3600 | 18000 | ||
| 10 | 250,3 | 792,7 | 1941,9 | 4342,4 | 15042,7 | 33636,4 | ||
| 11 | 155,8 | 494,5 | 1211,6 | 2709,4 | 9385,9 | 20987,5 | ||
| 12 | 95,2 | 303,5 | 744,1 | 1664 | 5764,4 | 12889,6 | ||
| 13 | 55,9 | 179,8 | 441,2 | 986,8 | 3418,5 | 7644 | ||
| 14 | 30,5 | 99,6 | 244,7 | 547,5 | 1896,9 | 4241,7 | ||
| 15 | 15 | 50 | 123,2 | 275,8 | 955,5 | 2136,6 | ||
| 16 | 6,7 | 22,8 | 56,2 | 125,9 | 436,1 | 975,2 | ||
| 17 | 2,8 | 9,7 | 23,9 | 53,6 | 185,6 | 415,1 | ||
| 18 | 1,2 | 4 | 9,8 | 22 | 76,1 | 170,2 | ||
| 19 | 0,5 | 1,6 | 4 | 8,8 | 30,7 | 68,6 | ||
| 20 | 0,2 | 0,6 | 1,6 | 3,5 | 12,3 | 27,4 | ||
| 21 | 0,1 | 0,3 | 0,6 | 1,4 | 4,9 | 10,9 | ||
| 22 | 0 | 0,1 | 0,3 | 0,6 | 1,9 | 4,4 | ||
| 23 | 0 | 0 | 0,1 | 0,2 | 0,8 | 1,7 | ||
| 24 | 0 | 0 | 0 | 0,1 | 0,3 | 0,7 | ||
| 25 | 0 | 0 | 0 | 0 | 0,1 | 0,3 | ||
| 26 | 0 | 0 | 0 | 0 | 0 | 0,1 | ||
| 27 | 0 | 0 | 0 | 0 | 0 | 0 | ||
Dans l'exemple ci dessus (site très fortement pollué correspondant à mon lieu d'observation habituel, fond de ciel mg 17 par secondes d'arc carrée) turbulence forte. La magnitude limite est proche de 21 après une heure de pose ce qui cadre bien avec mes conditions standards et mes résultats. La limite absolue est voisine de mg22 avec ce CCD.
Pour faire mieux il faut dans le même site:
_ Un télescope plus gros mais avec un 600mm on ne gagne pas grand chose par rapport à un 500mm
_ Un CCD avec un meilleur rendement quantique. Avec une KAF1603 on atteint en 1h la mg 22 et la mg22.9 en 5h
_ Une nuit avec faible turbulence
_ Le même télescope avec un fond de ciel de mg 22.5 et au pic du midi 2850m d'altitude atteint la magnitude 25.5 en 5h soit 2.6 magnitude de mieux!
Pour finir une comparaison avec des télescopes professionnels de grand diamètre. Les conditions sont: un site d'observatoire (mg ciel 22.5) une turbulence de 1" et le même CCD que pour l'exemple ci dessus avec un rendement quantique assez faible. Pose typique de 1h
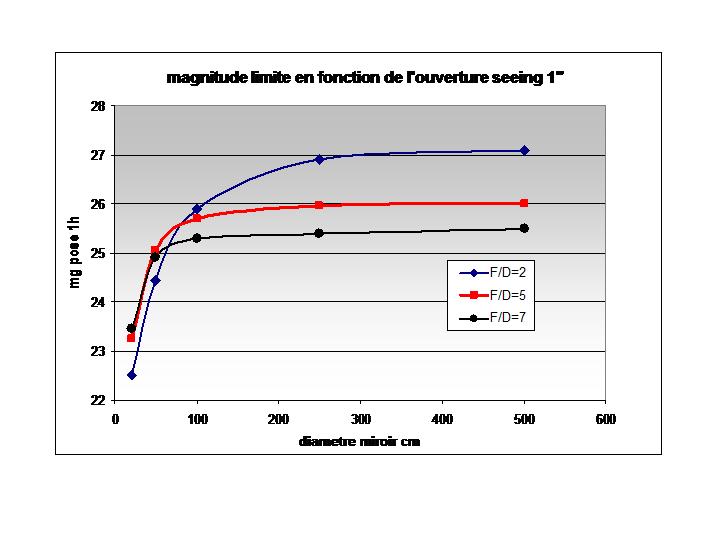
Comparaison de la magnitude atteinte pour plusieurs télescopes pixels 9µm pose 1h turbulence 1"
Il est intéressant de noter qu'avec de longues focales les télescopes de grands diamètres saturent vite. A F/D=7 un 5m ne fait pas mieux qu'un télescope de 1m cela provient du fait que ces télescopes sont limités par la turbulence et que l'échantillonnage du CCD n'est pas adapté à la focale du télescope. A F/D=2 par contre la courbe sature moins il y a plus d'énergie concentrée dans le pixel. On voit dans cette courbe toute la quête des instruments professionnels:
Très bon site sans turbulence, optique très ouverte, sinon on ne gagne rien. Un 8m ne fait pas mieux qu'un 5m sans cela !
Au niveau amateur jusqu'à 50cm il semble que les systèmes très ouverts ne sont pas les meilleurs au niveau magnitude limite. Il est intéressant de voir qu'un simple 200mm ouvert à F/D=5 ou 6 peut atteindre la magnitude 23.5 dans un très bon site.
Je vous encourage à vous amuser avec la feuille de calcul c'est très instructif et cela permet d'optimiser sont système voir de choisir une camera CCD.
Le flat field dont on n’a pas encore parlé sert à corriger les non uniformités de l'image associées au vignettage et à la différence de sensibilité des pixels.
Nmes(x,y)=K(x,y)Nimage(x,y)
K(x,y) est un coefficient proche de 1 comportant l’ensemble des non uniformités
Pour déterminer K(x, y) il faut donc disposer d’une image connue. Pour pouvoir restaurer l’image de départ on utilise donc une image uniforme de telle façon que Nimage (x,y)=C
K(x,y)=Nmes(x,y)/Nimage(x,y)=Nmes(x,y)/C
Donc deux problèmes: réaliser l’image constante et se préoccuper du bruit que ce nouveau traitement vas faire apparaître invariablement.
Le bruit de K(x,y) s’obtient à partir de l’équation (13) avec une considération spéciale pour la partie thermique. En effet les poses sont courtes donc avec un CCD bien refroidi ce terme est pratiquement négligeable et on a moins de bruit si on ne le soustrait pas ! Comme on veut avoir une photométrie correcte il est par contre indispensable de soustraire l’offset.
On peut donc écrire pour le signal :
Nflat = Nbrut - Nthermique ≈ Nbrut - Noffset
En moyennant n images brutes on obtient le flat maître
Nflat=1/n ∑ (Nbrut - Noffset)
et
K(x,y)=1/(nK) ∑ (Nbrut - Noffset)
K étant une constante qui représente la dynamique du flat. En effet notre facteur correctif est proche de 1
Le bruit du flat maître est
Bflat=1/n((n (Nflat+N2num (1+1/p)))1/2) = (Nflat+N2num (1+1/p))/n)1/2
Si on revient au traitement global de l’image on a :
Nbrut=K(x,y)Nphotons+Noffset+Nthermique
Nphotons=(Nbrut-Noffset-Nthermique)/K(x,y)
B=(Nphotons + Nciel + N2num(1+1/p) + N1thermique(1+1/p)+ Bflat2/K2)1/2
On voit que si la dynamique de l’image est grande (K grand) et le nombre d’images dans la moyenne est important le bruit induit par le flat Field est faible. Par contre il faut avoir une image constante de haute qualité pour ne pas rajouter des gradients de luminance dans l’image
L’image constante peut se faire de deux façons différentes:
On fait une image du fond de ciel à la tombée de la nuit ou au levé du jour à travers l’instrument
On utilise une boite à flat qui est un plan de lumière uniforme que l’on vient positionner à l’entrée du télescope.
Images du fond de ciel
C’est la méthode la plus économique et si on prends quelques précautions cela marche très bien. C’est en fait la seule méthode raisonnable pour un amateur possédant un gros télescopes.
La prise d’image se fait à la nuit tombante ou au lever du jour.
Pour éviter les non uniformités du fond de ciel il convient de pointer le télescope à 15° du zénith dans la direction opposée au soleil [16]. Le temps de pose ne doit pas être top court sinon un gradient dans l'image peut apparaître à cause de l'obturateur. Au fur et à mesure que le temps passe, la luminosité change et les étoiles peuvent apparaître si on fait ses images le soir. Pour éviter ces problèmes, le télescope n'est pas entraîné. Les étoiles si elles sont visible laissent des traînées qui seront éliminées au traitement. Le temps de pose est choisi pour avoir une dynamique correspondant environ au 3/4 de la valeur à saturation. Typiquement je fais une quinzaine d'images dans ces conditions avec un temps de pose inférieur à 10s et supérieur à 2 secondes. Pour réaliser le flat je fait l'image médiane de toutes les images après les avoir normalisées à une valeur moyenne constante. Les étoiles filées présentent dans l'image sont éliminées par ce traitement . Ensuite sur image médiane obtenue, je soustrais l'offset moyen.
Un point très important est qu'il ne faut absolument pas changer la camera de position entre les prises d'images et les flat. Mise au point identique, orientation identique. Étant à poste fixe je fais les flats à la tombée de la nuit suivant les prises d'images sans avoir rien changé depuis la veille.
Images avec une boite à flat
Compte tenu du diamètre de mon miroir je n'utilise pas cette méthode. On trouve aujourd'hui des plans lumineux de bonne qualité à des prix raisonnables pour des diamètres jusqu'a 200mm environ après c'est une question de budget .
Comparaison télescopes